Cho hai số thực a,b thỏa mãn Giá trị của a-tanb bằng
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Mệnh đề có dạng \(P \Rightarrow Q\) với P: “\(2a - 1 > 0\)” và Q: “\(a > 0\)”
Ta thấy khi P đúng (tức là \(a > \frac{1}{2}\)) thì Q cũng đúng. Do đó, \(P \Rightarrow Q\) đúng.
b) Mệnh đề có dạng \(P \Leftrightarrow Q\) với P: “\(a - 2 > b\)” và Q: “\(a > b + 2\)”
Khi P đúng thì Q cũng đúng, do đó, \(P \Rightarrow Q\) đúng.
Khi Q đúng thì P cũng đúng, do đó, \(Q \Rightarrow P\) đúng.
Vậy mệnh đề \(P \Leftrightarrow Q\) đúng.

Chọn D.
Phương pháp
Xét tính đúng sai của từng đáp án, chú ý các tính chất của logarit.
Cách giải:
Dễ thấy các đáp án A, B, C đều đúng theo tính chất logarit. Đáp án D sai vì chưa biết b > 0 hay b < 0 nên
không phá được dấu giá trị tuyệt đối trong đáp án D.

\(a< \sqrt{ab}\)
\(\Leftrightarrow a^2< ab\)
\(\Leftrightarrow a^2-ab< 0\)
\(\Leftrightarrow a\left(a-b\right)< 0\) (đúng) (1)
\(\sqrt{ab}< \dfrac{a+b}{2}\) (áp dụng BĐT AM-GM). (2)
\(\dfrac{a+b}{2}< b\)
\(\Leftrightarrow\dfrac{a}{2}-\dfrac{b}{2}< 0\)
\(\Leftrightarrow\dfrac{a-b}{2}< 0\) (đúng) (3)
-Từ (1), (2), (3) ta suy ra đpcm.
 .
. 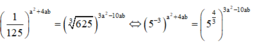
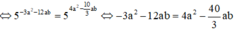
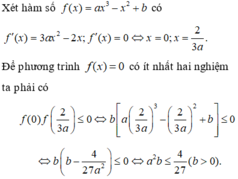



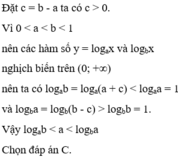
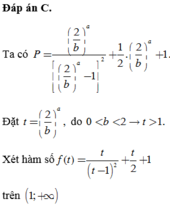
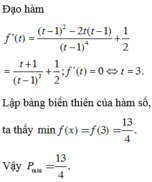
Có
Chọn đáp án C.