Cho phương trình 2 sin x - 1 3 tan x + 2 sin x = 3 - 4 cos 2 x . Tổng tất cả các nghiệm thuộc đoạn 0 ; 20 π của phương trình bằng
A. 1150 3 π
B. 570 3 π
C. 880 3 π
D. 875 3 π
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn C
Ta có: 
nên (1) và (2) có nghiệm.
Cách 1:
Xét: 
nên (3) vô nghiệm.
Cách 2:
Điều kiện có nghiệm của phương trình: sin x + cos x = 2 là: 
(vô lý) nên (3) vô nghiệm.
Cách 3:
Vì 
nên (3) vô nghiệm.
\(cosx-\left(3sinx-4sin^3x\right)=\sqrt{2}\left(cosx-sinx\right)sin4x\)
\(\Leftrightarrow cosx-sinx+2sinx\left(2sin^2x-1\right)=\sqrt{2}\left(cosx-sinx\right)sin4x\)
\(\Leftrightarrow cosx-sinx-2sinx\left(cosx-sinx\right)\left(cosx+sinx\right)=\sqrt{2}\left(cosx-sinx\right)sin4x\)
\(\Leftrightarrow\left(cosx-sinx\right)\left(1-2sinx\left(sinx+cosx\right)-\sqrt{2}sin4x\right)=0\)
\(\Leftrightarrow\left(cosx-sinx\right)\left(1-2sin^2x-2sinx.cosx-\sqrt{2}sin4x\right)=0\)
\(\Leftrightarrow\left(cosx-sinx\right)\left(cos2x-sin2x-\sqrt{2}sin4x=0\right)\)
\(\Leftrightarrow\left(cosx-sinx\right)\left[sin\left(\dfrac{\pi}{4}-2x\right)-sin4x\right]=0\)
\(\Leftrightarrow...\)
1.
ĐKXĐ: \(x\ne k\pi\)
\(\Leftrightarrow\left(2cos2x-1\right)\left(sinx-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos2x=\dfrac{1}{2}\\sinx=3>1\left(ktm\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=\dfrac{\pi}{3}+k2\pi\\2x=-\dfrac{\pi}{3}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k\pi\\x=-\dfrac{\pi}{6}+k\pi\end{matrix}\right.\)
2. Bạn kiểm tra lại đề, pt này về cơ bản ko giải được.
3.
ĐKXĐ: \(x\ne\dfrac{k\pi}{2}\)
\(\dfrac{3\left(sinx+\dfrac{sinx}{cosx}\right)}{\dfrac{sinx}{cosx}-sinx}-2cosx=2\)
\(\Leftrightarrow\dfrac{3\left(1+cosx\right)}{1-cosx}+2\left(1+cosx\right)=0\)
\(\Leftrightarrow\left(1+cosx\right)\left(\dfrac{3}{1-cosx}+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=-1\left(loại\right)\\cosx=\dfrac{5}{2}\left(loại\right)\end{matrix}\right.\)
Vậy pt đã cho vô nghiệm
a.
\(\left(sin^2\dfrac{x}{2}+cos^2\dfrac{x}{2}\right)^2-2sin^2\dfrac{x}{2}cos^2\dfrac{x}{2}=\dfrac{1}{2}\)
\(\Leftrightarrow2-\left(2sin\dfrac{x}{2}cos\dfrac{x}{2}\right)^2=1\)
\(\Leftrightarrow1-sin^2x=0\)
\(\Leftrightarrow cos^2x=0\)
\(\Leftrightarrow x=\dfrac{\pi}{2}+k\pi\)
b.
\(\left(sin^2x+cos^2x\right)^3-3sin^2x.cos^2x\left(sin^2x+cos^2x\right)=\dfrac{7}{16}\)
\(\Leftrightarrow1-\dfrac{3}{4}\left(2sinx.cosx\right)^2=\dfrac{7}{16}\)
\(\Leftrightarrow16-12.sin^22x=7\)
\(\Leftrightarrow3-4sin^22x=0\)
\(\Leftrightarrow3-2\left(1-cos4x\right)=0\)
\(\Leftrightarrow cos4x=-\dfrac{1}{2}\)
\(\Leftrightarrow4x=\pm\dfrac{2\pi}{3}+k2\pi\)
\(\Leftrightarrow x=\pm\dfrac{\pi}{6}+\dfrac{k\pi}{2}\)
\(sin^2x-2m.sinx.cosx-sinx.cosx+2mcos^2x=0\)
\(\Leftrightarrow sinx\left(sinx-cosx\right)-2mcosx\left(sinx-cosx\right)=0\)
\(\Leftrightarrow\left(sinx-cosx\right)\left(sinx-2m.cosx\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}sinx=cosx\\sinx=2m.cosx\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}tanx=1\\tanx=2m\end{matrix}\right.\)
Do \(tanx=1\) ko có nghiệm đã cho nên \(tanx=2m\) phải có nghiệm trên khoảng đã cho
\(\Rightarrow tan\left(\dfrac{\pi}{4}\right)< 2m< tan\left(\dfrac{\pi}{3}\right)\)
\(\Rightarrow1< 2m< \sqrt[]{3}\)
\(\Rightarrow m\in\left(\dfrac{1}{2};\dfrac{\sqrt{3}}{2}\right)\) (hoặc có thể 1 đáp án là tập con của tập này cũng được)
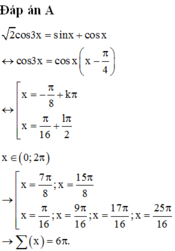
Chọn D.
Phương pháp:
- Sử dụng các công thức nhân ba, phân tích tích thành tổng để biến đổi đơn giản phương trình.
- Giải phương trình, tìm nghiệm thỏa mãn bài toán và tính tổng các nghiệm.