Question

[Pham Trong Bach]

Tìm giá trị nhỏ nhất của hàm số  $y=si{n}^{4}x+co{s}^{2}x+2.$

A. $\min y=3$

B. $\min y=\frac{11}{2}$

C. $\min y=-3$

D. $\min y=\frac{11}{4}$

Answer 1

[Cao Minh Tâm]

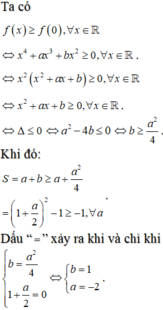
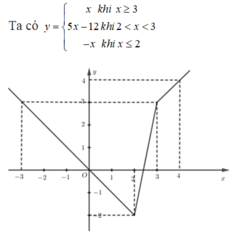
Đáp án là D.

Ta có:

y = sin 4 x + cos 2 x + 2 y = sin 4 x − sin 2 x + 3

Đăt  t = sin 2 x , t ∈ 0 ; 1

f ( t ) = t 4 − t 2 + 3 ⇒ f ' ( t ) = 4 t 3 − 2 t ⇒ f ' ( t ) = 0 ⇔ t = 0 ∈ [ 0 ; 1 ] t = 2 2 ∈ [ 0 ; 1 ] t = − 2 2 ∉ [ 0 ; 1 ] ⇒ f ( 0 ) = 3 ; f ( 1 ) = 3 ; f 2 2 = 11 4

Vậy giá trị nhỏ nhất của hàm số đã cho là: 11 4