Xét các số thực dương x, y thỏa mãn Tính giá trị nhỏ nhất của biểu thức
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Ta có ln x y = ln x + ln y ≥ ln x 2 + y
⇔ x y ≥ x 2 + y ⇔ y x - 1 ≥ x 2
Vì x = 1 không thỏa và y > 0 => x > 1
⇒ P = x y ≥ x 2 x - 1 + x = f x
X é t h à m s ố f x = x 2 x - 1 + x v ớ i x > 1
⇒ f ' x = x 2 - 2 x x - 1 2 + x = 2 x 2 - 4 x + 1 x - 1 2
⇒ f ' x = 0 ⇔ x = 2 + 2 2 v ì x > 1
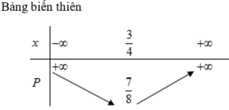
Dựa vào bảng biến thiên của hàm số f(x) suy ra
⇒ M i n P = M i n x > 1 f x = f 1 = 3 + 2 2 .

Đáp án A
ln 1 - 2 x x + y = 3 x + y - 1 , 0 < x < 1 2 , y > 0 ⇔ ln 1 - 2 x + 1 - 2 x = ln ( x + y ) + x + y f t = t + ln t ⇒ f ' t = 1 + 1 t > 0 ⇒ f 1 - 2 x = f ( x + y ) ⇔ 1 - 2 x = x + y ⇔ y = 1 - 3 x P = 1 x + 1 x y = 1 x + 1 x 1 - 3 x ⇒ P ' = - 1 x 2 + 6 x - 1 2 x 1 - 3 x x ( 1 - 3 x ) = - 2 x 1 - 3 x ( 1 - 3 x ) + ( 6 x - 1 ) x 2 x 1 - 3 x x 2 ( 1 - 3 x ) P ' = 0 ⇔ 2 x 1 - 3 x ( 1 - 3 x ) = 6 x 2 - x ⇔ 6 x 2 - x > 0 4 x ( 1 - 3 x ) 3 = 6 x 2 - x 2 ⇔ [ x < 0 x > 1 6 4 x - 36 x 2 + 108 x 3 - 108 x 4 = 26 x 4 - 12 x 3 + x 2 ⇔ x = y = 1 4 ⇒ P = 8

Đáp án B.
Từ giả thiết, suy ra
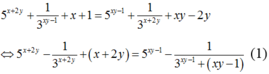
Xét hàm số f ( t ) = 5 t - 1 3 t + t trên ℝ .
Đạo hàm f ' ( t ) = 5 t . ln 5 - ln 3 3 t + 1 > 0 , ∀ t ∈ ℝ ⇒ hàm số f ( t ) luôn đồng biến trên ℝ .
Suy ra
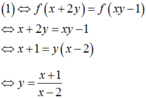
Do y > 0 nên x + 1 x - 2 > 0 ⇔ [ x > 2 x < - 1 . Mà x > 0 nên x > 2 .
Từ đó T = x + y = x + x + 1 x - 2 . Xét hàm số g ( x ) = x + x + 1 x - 2 trên 2 ; + ∞ .
Đạo hàm
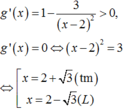
Lập bảng biến thiên của hàm số trên 2 ; + ∞ , ta thấy min g ( x ) = g ( 2 + 3 ) = 3 + 2 3 .
Vậy T m i n = 3 + 2 3 khi x = 2 + 3 và x = 1 + 3 .
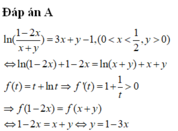
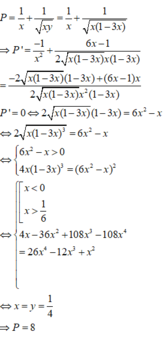
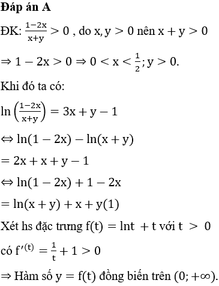

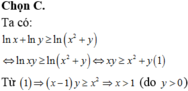

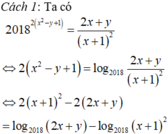
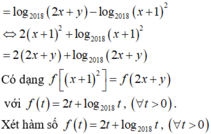

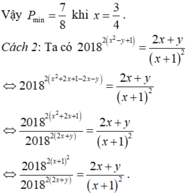


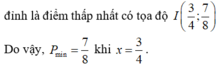


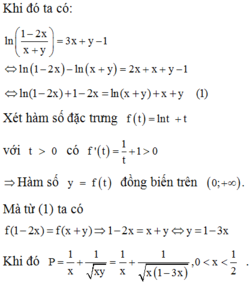

Đáp án A
ln ( 1 − 2 x x + y ) = 3 x + y − 1 , ( 0 < x < 1 2 , y > 0 ) ⇔ ln ( 1 − 2 x ) + 1 − 2 x = ln ( x + y ) + x + y f ( t ) = t + ln t ⇒ f ' ( t ) = 1 + 1 t > 0 ⇒ f ( 1 − 2 x ) = f ( x + y ) ⇔ 1 − 2 x = x + y ⇔ y = 1 − 3 x