Tìm họ nguyên hàm F(x) của hàm số
f
(
x
)
=
x
3
+
x
+
1
...
Đọc tiếp
Tìm họ nguyên hàm F(x) của hàm số
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 3 2022
Từ giả thiết: \(\int f\left(x\right).e^{2x}dx=x.e^x+C\)
Đạo hàm 2 vế:
\(\Rightarrow f\left(x\right).e^{2x}=e^x+x.e^x\)
\(\Rightarrow f\left(x\right)=\dfrac{e^x+x.e^x}{e^{2x}}=\dfrac{x+1}{e^x}\)
Xét \(I=\int f'\left(x\right)e^{2x}dx\)
Đặt \(\left\{{}\begin{matrix}u=e^{2x}\\dv=f'\left(x\right)\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=2.e^{2x}dx\\v=f\left(x\right)\end{matrix}\right.\)
\(\Rightarrow I=f\left(x\right).e^{2x}-2\int f\left(x\right).e^{2x}dx=\left(\dfrac{x+1}{e^x}\right)e^{2x}-2.x.e^x+C\)
\(=\left(1-x\right)e^x+C\)
CM
9 tháng 4 2019
Đáp án C
Có f x = x + 1 x − 1
Nguyên hàm của f(x) là F x = x 2 2 + ln x − 1 + C .
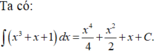
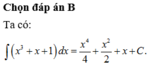
Chọn B