Cho đồ thị (C) của hàm số y' = ( 1 + x ) x + 2 2 x - 3 3 ( 1 - x 2 ) . Trong các mệnh đề sau, tìm mệnh đề sai:
A. (C) có một điểm cực trị.
B. (C) có ba điểm cực trị.
C. (C) có hai điểm cực trị.
D. (C) có bốn điểm cực trị.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D
Ta có: y ' = 3 x 2 - 4 x , y ' ' = 6 x - 4 ;
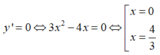
y''(0) = -4 < 0; y''(4/3) = 4 > 0. Do đó hàm số có hai cực trị là x = 0 và x = 4/3
Các mệnh đề (1); (2) và (3) sai;mệnh đề (4) đúng.

Chọn C
Dựa vào định nghĩa mệnh đề 1 sai và mệnh đề 2, 3, 4 đúng.

Đáp án B
Sai lầm thường gặp: Tập xác định D = ℝ \ 3 .
Đạo hàm y ' = − 2 x − 3 2 ,0, ∀ x ∈ D ⇒ Hàm số nghịch biến trên ℝ \ 3 , hoặc làm số nghịch biến trên − ∞ ; 3 ∪ 3 ; + ∞ . Hàm số không có cực trị.
Tiệm cận đứng: x=3; tiệm cận ngang: y=1. Đồ thị hàm số nhận giao điểm I 3 ; 1 của hai đường tiệm cận làm tâm đối xứng.
Từ đó nhiều học sinh kết luận các mệnh đề 1 , 3 , 4 đúng và chọn ngay A.
Tuy nhiên đây là phương án sai.
Phân tích sai lầm:
Mệnh đề (1) sai, sửa lại: hàm số nghịch biến trên mỗi khoảng − ∞ ; 3 và 3 ; + ∞ . Học sinh cần nhớ rằng, ta chỉ học định nghĩa hàm số đồng biến (nghịch biến) trên khoảng, đoạn, nửa khoảng; chứ không có trên những khoảng hợp nhau.
Mệnh đề (2) sai. Đồ thị hàm số có một tiệm cận đứng là x=3, một tiệm cận ngang là y=1.
Mệnh đề 3 , 4 đúng.

Đáp án D
Phương pháp: +) Khảo sát sự biến thiên của đồ thị hàm số.
+) Hàm số đạt cực trị tại điểm x = x 0 ⇔ y ' x 0 = 0 và x = x 0 được gọi là điểm cực trị.
+) Hàm số đạt cực trị tại điểm x = x 0 thì y x 0 là giá trị cực trị.


Như vậy có 3 mệnh đề đúng.
Chú ý: Học sinh thường giá trị cực trị và
điểm cực trị nên có thể chọn sai mệnh dề (2) đúng.

Đáp án C
Dựa vào đáp án, ta thấy rằng
(1) Đường thẳng f x = 0 ⇔ 3 2 x - 2 . 3 x = 0 ⇔ 3 x = 2 ⇔ x = log 3 2 ⇒ 1 đúng.
(2) Bất phương trình f x ≥ - 1 ⇔ 3 2 x - 2 . 3 x + 1 ≥ 0 ⇔ 3 x - 1 2 ≥ 0 , ∀ x ∈ ℝ . Nên f x ≥ - 1 có vô số nghiệm ⇒ 2 sai.
(3) Bất phương trình f x ≥ 0 ⇔ 3 x 2 - 2 . 3 x ≥ 0 ⇔ 3 x ≥ 2 ⇔ x ≥ log 3 2 ⇒ 3 sai.
(4) Đường thẳng f(x) = 0 chỉ có 1 nghiệm duy nhất ⇒ 4 sai
Chọn C.
Ta có y' = ( 1 + x ) x + 2 2 x - 3 3 ( 1 - x 2 ) nên y' = 0
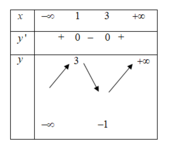
Bảng xét dấu
Ta thấy đạo hàm đổi dấu 2 lần nên hàm số có hai điểm cực trị suy ra đồ thị hàm số có 2 điểm cực trị.
Trắc nghiệm: Ta thấy phương trình y' = 0 có 2 nghiệm đơn hoặc bội lẻ nên đồ thị hàm số có hai điểm cực trị.