Biết số phức z thỏa mãn điều kiện và biểu thức đạt giá trị lớn nhất. Tính
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D.
Đặt z = x + yi (x,y ∈ Z) => Tập hợp các điểm M là đường tròn (C) có tâm I(3;4), bán kính R = 5
Ta có ![]()
![]()
![]()
![]()
Ta cần tìm P sao cho đương thẳng (∆) và đường tròn (C) có điểm chung ó d(I;( ∆))≤ R
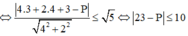
![]()
Do đó maxP = 33. Dấu “=” xảy ra 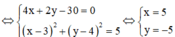
Vậy |z| = 5 2

Tập hợp các điểm z thỏa mãn điều kiện z - 1 = 2 là đường tròn (C) tâm I(1;0) bán kính R = 2
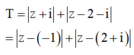
Gọi M là điểm biểu diễn cho số phức z, A(0,-1) là điểm biểu diễn cho số phức -i, B(2;1)là điểm biểu diễn cho số phức 2+i

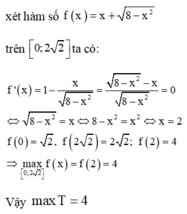
Đáp án D

Đáp án D
Phương pháp: Đưa biểu thức T về dạng biểu thức vector bằng cách tìm các vecto biểu diễn cho các số phức.
Cách giải:
Tập hợp các điểm z thỏa mãn điều kiện ![]() là đường tròn (C) tâm I(1;0) bán kính R=
2
là đường tròn (C) tâm I(1;0) bán kính R=
2
![]()
Gọi M là điểm biểu diễn cho số phức z, A(0;-1) là điểm biểu diễn cho số phức -i, B(2;1) là điểm biểu diễn cho số phức 2+i
Dễ thấy A,B
∈
C và ![]()
![]() AB là đường kính của đường tròn (C)
AB là đường kính của đường tròn (C)
![]() vuông tại M
vuông tại M
![]()
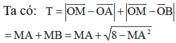
Đặt ![]()
Xét hàm số ![]() trên
trên ![]() ta có:
ta có:
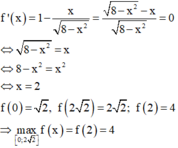
Vậy maxT=4

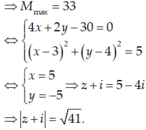
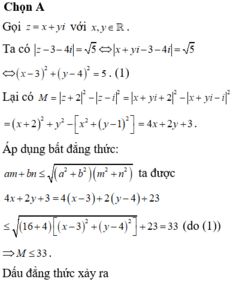
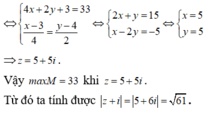


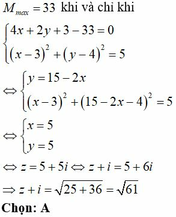

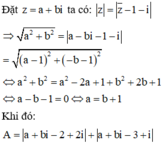
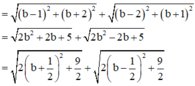
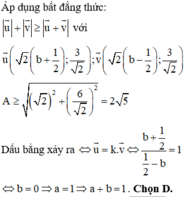
Đáp án D.