Trong mặt phẳng tọa độ Oxy, cho đường thẳng . Một vectơ chỉ phương của đường thẳng là:
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



1: (d): x=-2-2t và y=1+2t nên (d) có VTCP là (-2;2)=(-1;1) và đi qua B(-2;1)
=>(d') có VTPT là (-1;1)
Phương trình (d') là;
-1(x-3)+1(y-1)=0
=>-x+3+y-1=0
=>-x+y+2=0
2: (d) có VTCP là (-1;1)
=>VTPT là (1;1)
Phương trình (d) là:
1(x+2)+1(y-1)=0
=>x+y+1=0
Tọa độ H là;
x+y+1=0 và -x+y+2=0
=>x=1/2 và y=-3/2

a: 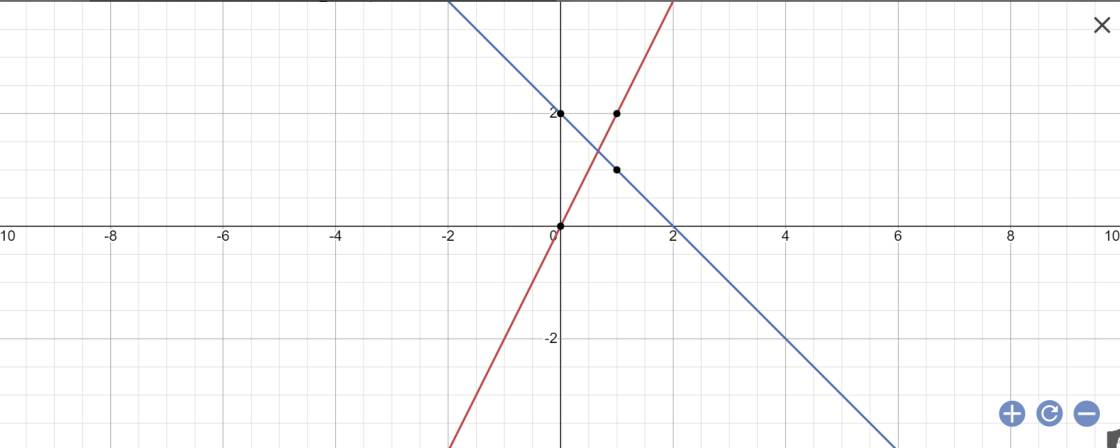
b: Vì (d3)//(d2) nên \(\left\{{}\begin{matrix}a=-1\\b\ne2\end{matrix}\right.\)
Vậy: (d3): y=-x+b
Thay x=1 vào (d1), ta được:
\(y=2\cdot1=2\)
Thay x=1 và y=2 vào y=-x+b, ta được:
\(b-1=2\)
=>b=2+1=3

a/ CD qua E và vuông góc BC nên pt có dạng:
\(1\left(x-6\right)-1\left(y-0\right)=0\Leftrightarrow x-y-6=0\)
Ta có: \(AB=d\left(A;BC\right)=\frac{\left|3+5-2\right|}{\sqrt{1^2+1^2}}=3\sqrt{2}\)
\(AD=d\left(A;CD\right)=\frac{\left|3-5-6\right|}{\sqrt{1^2+\left(-1\right)^2}}=4\sqrt{2}\)
\(\Rightarrow S_{ABCD}=AB.AD=24\)
b/ Do M thuộc d nên tọa độ có dạng: \(M\left(1+t;2-3t\right)\)
Áp dụng công thức khoảng cách:
\(d\left(M;\Delta\right)=4\Leftrightarrow\frac{\left|3\left(1+t\right)+4\left(2-3t\right)+5\right|}{\sqrt{3^2+4^2}}=4\)
\(\Leftrightarrow\left|16-9t\right|=20\Rightarrow\left[{}\begin{matrix}16-9t=20\\16-9t=-20\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}t=-\frac{4}{9}\\t=4\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}M\left(\frac{5}{9};\frac{10}{3}\right)\\M\left(5;-10\right)\end{matrix}\right.\)

1: Để hai đường song song thì m+3=2
hay m=-1
Bạn ơi, bạn kí hiệu lại đi bạn. Khó hiểu quá

(*)Tọa độ giao điểm là nghiệm của hệ \(\left\{\begin{matrix}y=-mx-1\\x+y=-m\end{matrix}\right.\)
\(\Leftrightarrow\left\{\begin{matrix}\left(1-m\right)x=1-m\\\left(1-m\right)y=m^2-1\end{matrix}\right.\)
Nếu m=1 =>No với mọi x,y => hai đường thẳng trùng loại nhau:Nghiệm duy nhất=> m khác 1
khi m khác 1 ta có: \(\left\{\begin{matrix}x=1\\y=\frac{1}{m+1}\end{matrix}\right.\)
tọa độ giao diểm là: \(A\left(1,\frac{1}{m+1}\right)\)
(**) thỏa mãn: \(y^2+2006x\ge2010\)
\(\Leftrightarrow\left(\frac{1}{m+1}\right)^2+2009.1\ge2010\Rightarrow\left(\frac{1}{m+1}\right)^2\ge1\Rightarrow\left(m+1\right)^2\le1\)
\(\Rightarrow-1\le m+1\le1\Leftrightarrow-2\le m\le0\)

Thay M(1 ; -2 ) vào đồ thị hàm số, ta có :
a + b = -2 (1)
Vì (d) song song với đường thẳng y= x+1
=> \(\left\{{}\begin{matrix}a=1\\b\ne1\end{matrix}\right.\)( 2 )
Kết hợp (1) với (2) :
\(\left\{{}\begin{matrix}a+b=-2\\a=1\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}a=1\\b=-3\end{matrix}\right.\) ( thỏa mãn )
Vậy với a = 1 và b = -3 thì (d) đi qua M(1; -2 ) và song song với đường thẳng y = x+1