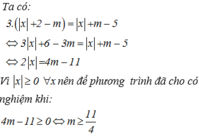Tập tất cả các giá trị thức của tham số m để vô nghiệm là
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

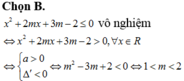

2: \(\text{Δ}=1^2-4\cdot\left(-1\right)\cdot\left(-m\right)=1-4m\)
Để bất phương trình vô nghiệm thì \(\left\{{}\begin{matrix}1-4m< 0\\-1< 0\end{matrix}\right.\Leftrightarrow m>\dfrac{1}{4}\)

Câu 2 bạn ghi thiếu đề
Câu 1:
\(\Leftrightarrow\left(m^2-3m\right)x+2x< 2-m\)
\(\Leftrightarrow\left(m^2-3m+2\right)x< 2-m\)
BPT đã cho vô nghiệm khi và chỉ khi:
\(\left\{{}\begin{matrix}m^2-3m+2=0\\2-m\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m=1\\m=2\end{matrix}\right.\\m\ge2\end{matrix}\right.\) \(\Rightarrow m=2\)

\(x^2-2\left(m-1\right)x+4m+8< 0\)
\(\text{Δ}=\left[-2\left(m-1\right)\right]^2-4\cdot1\cdot\left(4m+8\right)\)
\(=4m^2-4m+1-16m+32\)
\(=4m^2-20m+33\)
Để BPT vô nghiệm thì \(\left\{{}\begin{matrix}\text{Δ}< =0\\a>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}4m^2-20m+33< =0\\1>0\left(đúng\right)\end{matrix}\right.\)
=>\(4m^2-20m+33< =0\)
=>\(\left(2m-5\right)^2+8< =0\)(vô lý)
=>\(m\in\varnothing\)

TH1: m+1=0 <=> m=-1
Khi đó bpt là -2(-1+1)x+4 >= 0 <=> -4x+4 >= 0 <=> x<=1 (KTM S=R) => loại
TH2: m+1 khác 0 <=> m khác -1
Để bpt (m+1)x2 -2(m+1)x+4 ≥ 0 có nghiệm với mọi x
<=> {a>0Δ′≤0⇔{m+1>0[−(m+1)]2−4(m+1)≤0{a>0Δ′≤0⇔{m+1>0[−(m+1)]2−4(m+1)≤0
<=>{

\(\Leftrightarrow3\left|x-1\right|+6-3m=\left|x-1\right|+m-5\)
\(\Leftrightarrow2\left|x-1\right|=4m-11\)
Do \(2\left|x-1\right|\ge0\) với mọi x nên pt có nghiệm khi:
\(4m-11\ge0\Rightarrow m\ge\dfrac{11}{4}\)

Trường hợp 1: m=-1
Bất phương trình sẽ là \(0x^2-2\cdot0\cdot x+4>=0\)(luôn đúng)
Trường hợp 2: m<>-1
\(\text{Δ}=\left(2m+2\right)^2-4\cdot4\cdot\left(m+1\right)\)
\(=4m^2+8m+4-16m-16\)
\(=4m^2-8m-12\)
\(=4\left(m^2-2m-3\right)\)
Để bất phương trình có nghiệm đúng với mọi x thực thì \(\left\{{}\begin{matrix}\left(m-3\right)\left(m+1\right)< 0\\\left(m+1\right)>=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-1< m< 3\\m>=-1\end{matrix}\right.\Leftrightarrow-1< m< 3\)
Vậy: -1<=m<3