Tìm tất cả các giá trị thực của tham số m để hàm số y = m 3 x 3 − m + 1 x 2 + m − 2 x − 3 m nghịch biến trên khoảng − ∞ ; + ∞ .
A. − 1 4 ≤ m < 0
B. m ≤ − 1 4
C. m<0
D. m>0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AM
14 tháng 2 2022
Để y xác định thì \(\left(m-2\right)x+2m-3\ge0\forall x\in\left[-1;4\right]\)
\(\Leftrightarrow mx-2x+2m-3\ge0\)
\(\Leftrightarrow m\left(x+2\right)-2x-3\ge0\)
\(\Leftrightarrow m\ge\dfrac{2x+3}{x+2}\left(x+2>0\forall x\in\left[-1;4\right]\right)\)
\(\Rightarrow1\le m\le\dfrac{11}{6}\)
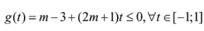
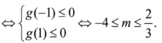
Đáp án B
Ta có y ' = m x 2 − 2 m + 1 x + m − 2. Hàm số nghịch biến trên − ∞ ; + ∞ ⇔ y ' ≤ 0 , ∀ x ∈ − ∞ ; + ∞ .
TH1: m = 0 ⇒ y ' ≤ 0 ⇔ − 2 x − 2 ≤ 0 ⇔ x ≥ − 1 ⇒ hàm số không nghịch biến trên − ∞ ; + ∞
TH2: m ≠ 0 ⇒ y ' ≤ 0 , ∀ x ∈ − ∞ ; + ∞ ⇔ m < 0 Δ ' y ' ≤ 0 ⇔ m < 0 m + 1 2 − 3 m m − 2 ≤ 0 ⇔ m < 0 m ≤ − 1 4 ⇒ m ≤ − 1 4 Kết hợp 2 TH, suy ra m ≤ − 1 4 .