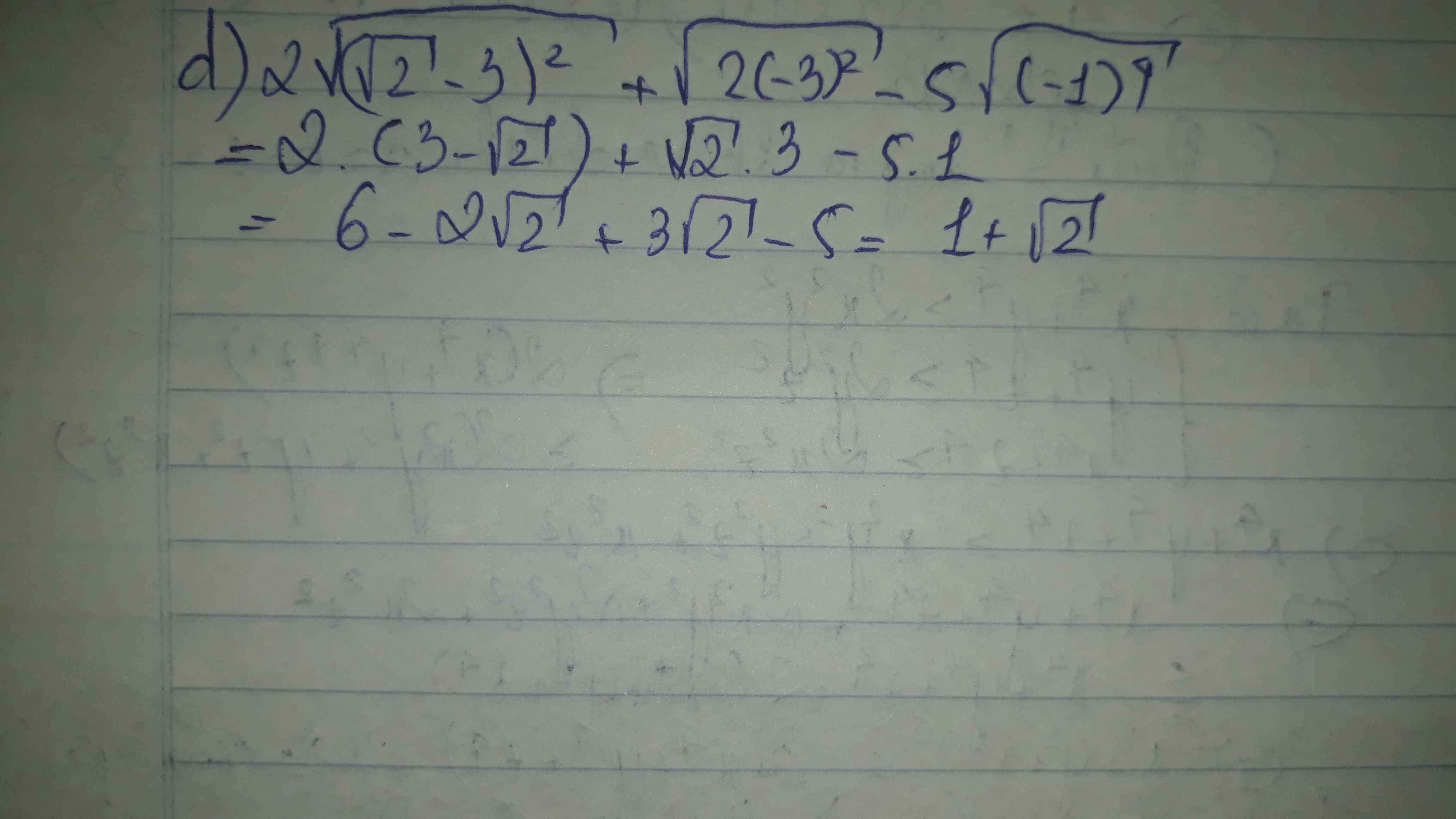Rút gọn các biểu thức: 2 - 3 2 + 4 + 2 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

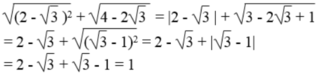

a,M=2^0-2^1+2^2-2^3+2^4-2^5+.....+2^2012
2M=2^1-2^2+2^3-2^4+2^5-2^5+......-2^2012+2^2013
3M=2^0+2^2013
M=(2^0+2^2013)÷3
Vậy.......
b,N=3-3^2+3^3-3^4+3^5-3^6+.....+3^2011-3^2012
3N=3^2-3^3+3^4-3^5+3^6-3^7+......+3^2012-3^2013
4N=3-3^2013
N=(3-3^2013)÷4
Vậy........
K tao nhé ko lên lớp tao đánh m😈😈😈

Bài 1:
a: \(A=\dfrac{x^2-3+x+3}{\left(x-3\right)\left(x+3\right)}\cdot\dfrac{x+3}{x}=\dfrac{x\left(x+1\right)}{x\left(x-3\right)}=\dfrac{x+1}{x-3}\)
b: Để A=3 thì 3x-9=x+1
=>2x=10
hay x=5
Bài 2:
a: \(A=\dfrac{x+x-2-2x-4}{\left(x-2\right)\left(x+2\right)}:\dfrac{x+2-x}{x+2}\)
\(=\dfrac{-6}{x-2}\cdot\dfrac{1}{2}=\dfrac{-3}{x-2}\)
b: Để A nguyên thì \(x-2\in\left\{1;-1;3;-3\right\}\)
hay \(x\in\left\{3;1;5;-1\right\}\)


`Answer:`
`a)`
`A=5(x+1)^2-3(x-3)^2-4(x^2-4)`
`=>A=5(x^2+2x+1)-3(x^2-6x+9)-4x^2+16`
`=>A=5x^2+10x+5-3x^2+18x-27-4x^2+16`
`=>A=(5x^2-3x^2-4x^2)+(10x+18x)+(5-27+16)`
`=>A=-2x^2+28x-6`
`b)`
`B=5(x+1)^2-3(x-3)^2-4(x+2)(x-2)`
`=2x(3x+5)-3(3x+5)-2x(x^2-4x+4)-[(2x)^2-3^2]`
`=6x^2+10x-9x-15-2x^3+8x^2-8x-4x^2+9`
`=(6x^2-4x^2+8x^2)-2x^3+(10x-9x-8x)+(-15+9)`
Thay `x=-7` vào ta được:
`B=10(-7)^2-2(-7)^3-7(-7)-6`
`=>B=10.49-2(-343)+49-6`
`=>B=490+686+49-6`
`=>B=1219`

1/2 x 2 (6x – 3) – x( x 2 + 1/2) + 1/2.(x + 4)
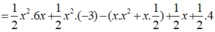
= (3 x 3 – 3/2. x 2 ) – ( x 3 + 1/2.x) + (1/2.x + 2)
= 3 x 3 - 3/2 x 2 – x 3 - 1/2 x + 1/2 x + 2
= ( 3 x 3 – x 3 ) - 3/2. x 2 – (1/2 x - 1/2 x) + 2
= 2 x 3 - 3/2 x 2 + 2

1) \(\left(x+1\right)^3-\left(x-4\right)\left(x+4\right)-x^3\)
\(=\left(x^3+3x^2+3x+1\right)-\left(x^2-16\right)-x^3\)
\(=x^3+3x^2+3x+1-x^2+16-x^3\)
\(=2x^2+3x+17\)
2) \(\left(x+2\right)^3-x\left(x+3\right)\left(x-3\right)-12x^2-8\)
\(=\left(x^3+6x^2+12x+8\right)-x\left(x^2-9\right)-12x^2-8\)
\(=x^3+6x^2+12x+8-x^3+9x-12x^2-8\)
\(=-6x^2+21x\)
`@` `\text {Ans}`
`\downarrow`
`1.`
\((x + 1) ^ 3 - (x - 4)(x + 4) - x ^ 3\)
`= x^3 + 3x^2 + 3x + 1 - [ x(x+4) - 4(x+4)] - x^3`
`= x^3 + 3x^2 + 3x + 1 - (x^2 + 4x - 4x - 16) - x^3`
`= x^3 + 3x^2 + 3x + 1 - (x^2 - 16) - x^3`
`= x^3 + 3x^2 + 3x + 1 - x^2 + 16 - x^3`
`= (x^3 - x^3) + (3x^2 - x^2) + 3x + (1+16)`
`= 2x^2 + 3x + 17`
`2.`
\((x + 2) ^ 3 - x(x + 3)(x - 3) - 12x ^ 2 - 8\)
`= x^3 + 6x^2 + 12x + 8 - [ (x^2 + 3x)(x-3)] - 12x^2 - 8`
`= x^3 + 6x^2 + 12x + 8 - (x^3 - 9x) - 12x^2 - 8`
`= x^3 + 6x^2 + 12x +8 - x^3 + 9x - 12x^2 - 8`
`= (x^3 - x^3) + (6x^2 - 12x^2) + (12x + 9x) + (8-8)`
`= -6x^2 + 21x `

\(=2\left|3-\sqrt{2}\right|+\sqrt{18}-5.1=6-2\sqrt{2}+3\sqrt{2}-5\)
\(=1+\sqrt{2}\)

a: \(=2\sqrt{2}+1-3=2\sqrt{2}-2\)
b: \(=\sqrt{3}+1-2\sqrt{3}-1=-\sqrt{3}\)
c: \(=2-\sqrt{3}+\sqrt{3}-1=1\)

\(\dfrac{x^2-4x+4}{x^3-2x^2-\left(4x-8\right)}=\dfrac{\left(x-2\right)^2}{x^3-2x^2-4x+8}\)
Để biểu thức trên nhận giá trị âm khi \(\dfrac{\left(x-2\right)^2}{x^3-2x^2-4x+8}< 0\)
\(\Rightarrow x^3-2x^2-4x+8< 0\)do \(\left(x-2\right)^2\ge0\)
\(\Leftrightarrow\left(x+2\right)\left(x^2-2x+4\right)-2x\left(x+2\right)< 0\)
\(\Leftrightarrow\left(x+2\right)\left(x-2\right)^2< 0\Leftrightarrow x< -2\)

a)
`4*(2y+3x)-3(x-3y)`
`=8y+12x-3x+9y`
`=8y+9y+12x-3x`
`=17y+9x`
b)
`x^2 +2x-x(7x-3)`
`=x^2 +2x-7x^2 +3x`
`=x^2 -7x^2 +2x+6x`
`= -6x^2 +8x`