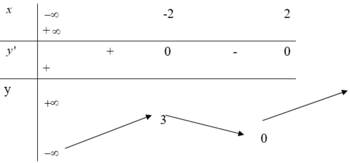
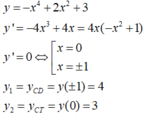Cho hàm số có giá trị cực tiểu lần lượt là Khi đó bằng
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

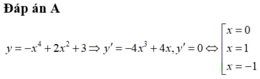

Chọn A.

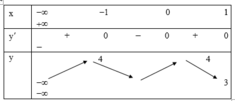
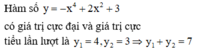
Chú ý: Cần phân biệt điểm cực đại và giá trị cực đại cũng như điểm cực tiểu và giá trị cực tiểu của hàm số.

Đáp án C
Ta có y ' = 3 x 2 − 6 x = 0 ⇔ x = 0 ⇒ y = − 2 = a x = 2 ⇒ y = − 6 = b
Khi đó 2 a 2 + b = 2

Đáp án A
y ' = x 2 + 4 x + 3 x + 2 2 ⇒ y ' = 0 ⇔ x 2 + 4 x + 3 = 0 ⇔ x = − 1 ⇒ y c t = 1 = n x = − 3 ⇒ y c d = − 3 = M ⇒ M 2 − 2 n = 7

Chọn B
![]()
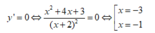
Hàm số đạt cực đại tại x=-3 và y y C D = - 3
Hàm số đạt cực tiểu tại x=-1 và y C T = 1
⇒ M 2 - 2 n = 7
Phương pháp trắc nghiệm:
Bấm máy tính:
Bước 1
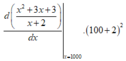
![]()
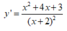
Bước 2: Giải phương trình bậc hai :
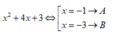
Bước 3: Nhập vào máy tính
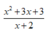
Cacl x = A → C
Cacl x = B → D
Bước 4: Tính C 2 - 2 D = 7

Ta có \(y'=3x^2-3\left(m-2\right)x-3\left(m-1\right)\), với mọi \(x\in R\)
\(y'=0\Leftrightarrow x^2-\left(m-2\right)x-m+1=0\Leftrightarrow x_1=-1;x_2=m-1\)
Chú ý rằng với m > 0 thì \(x_1< x_2\). Khi đó hàm số đạt cực đại tại \(x_1=-1\) và đạt cực tiểu tại \(x_2=m-1\). Do đó :
\(y_{CD}=y\left(-1\right)=\frac{3m}{2};y_{CT}=y\left(m-1\right)=-\frac{1}{2}\left(m+2\right)\left(m-1\right)^2+1\)
Từ giả thiết ta có \(2.\frac{3m}{2}-\frac{1}{2}\left(m+2\right)\left(m-1\right)^2+1\Leftrightarrow6m-6-\left(m+2\right)\left(m-1\right)^2=0\)
\(\Leftrightarrow\left(m-1\right)\left(m^2+m-8\right)=0\Leftrightarrow m=1;m=\frac{-1\pm\sqrt{33}}{2}\)
Đối chiếu yêu cầu m > 0, ta có giá trị cần tìm là \(m=1;m=\frac{-1\pm\sqrt{33}}{2}\)

Giá trị cực đại bằng y(-2)=3 giá trị cực tiểu bằng y(2)=0
Chọn đáp án D.