Cho ba tia chung gốc Ox, Oy và Oz sao cho và . Trong ba tia này có tia nào nằm giữa hai tia còn lại không?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có y O z ^ + x O z ^ = z O y ^ (cùng bằng 130°). Vậy tia Oz nằm giữa hai tia Ox và Oy.

a/vì \(60^o< 130^o\)hay \(\widehat{xOy}< \widehat{xOz}\)
nên Oy nằm giữa 2 tia Ox à Oz
b/ta có: góc xOy+góc yOz=xOz
=>góc yOz=góc xOz-góc xOy=130o-60o=70o
vì 70o>60onên góc yOz>góc xOy
c/ta có Ox' là tia đối của Ox
=> góc xOx'=180o
=>góc xOz+góc zOx'=180o
=> góc zOx'=60o

\(\Rightarrow\)tia oz nằm giữa 2 tia còn lại
hzmmmmm
(^_^)
{>@}

Có góc xOt + góc yOt=180' (2 gocke bu)
130' + góc yOt =180'
goc yOt=180'-130'
gocyOt=50'
Có góc yOt+góc tOz=góc yOz(Ot nằm giữa Oz và Oy)
50'+goctOz=100'
góc tOz=100'-50'
góc tOz=50'

Bạn tham khảo cách của mình nhé :D
Ta có 3 tia Ox ; Oy ; Oz chung gốc O
Lại có \(\widehat{xOz}=70^o;\widehat{yOz}=30^o\)
⇒ \(\widehat{xOz}>\widehat{yOz}\)
⇒ Ta sẽ có 2 trường hợp hình vẽ như sau
Trường hợp 1 : Oz nằm giữa Oy và Ox
O x z y 30 70
Khi Oz nằm giữa Oy và Ox thì ta được đẳng thức sau :
\(\widehat{xOy}=\widehat{yOz}+\widehat{yOx}\)
⇒ \(40^o=30^o+70^o\) ( vô lí)
Trường hợp 2 : Oy nằm giữa Ox và Oy
z O y x 30 40
Khi Oy nằm giữa Ox và Oy thì ta lại có đẳng thức
\(\widehat{xOy}+\widehat{yOz}=\widehat{xOz}\)
⇒ 30o + 40o = 70o ( hợp lí)
Vậy Oy....
P/s : có lẽ bạn sẽ thắc mắc tại s lại sra đc 2 trường hợp đó pk ko ạ ? __

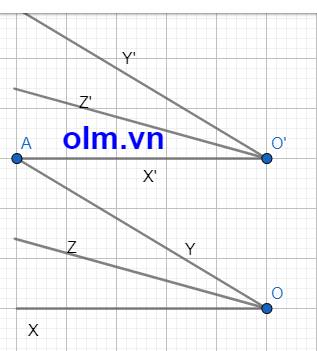
a,Kéo dài OY cắt O'X' tại A ta có:
\(\widehat{XOY}\) = \(\widehat{XOA}\) = \(\widehat{OAO'}\) (so le trong) (1)
\(\widehat{Y'O'X'}\) = \(\widehat{Y'O'A}\) = \(\widehat{OAO'}\) (so le trong) (2)
Kết hợp (1) Và (2) ta có:
\(\widehat{XOY=}\) \(\widehat{X'O'Y'}\) (đpcm)
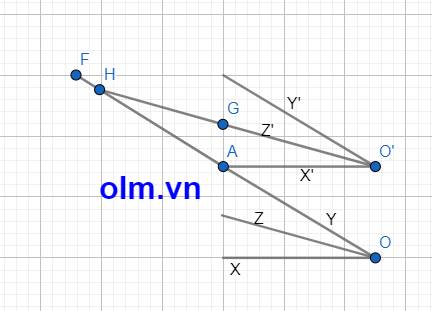
b, Kéo dài OY cắt O'Z' tại H
\(\widehat{ZOA}\) = \(\dfrac{1}{2}\) \(\widehat{XOY}\) (vì OZ là phân giác của góc XOY
\(\widehat{HO'A}\) = \(\dfrac{1}{2}\) \(\widehat{X'O'Y'}\) (vì OY là phân giác của góc X'O'Y')
Mặt khác ta có \(\widehat{OAO'}\) = \(\widehat{HO'A}\) + \(\widehat{AHO'}\) (góc ngoài tam giác bằng tổng hai góc trong không kề với nó)
\(\widehat{HO'A}\) = \(\dfrac{1}{2}\) \(\widehat{OAO'}\) ⇒ \(\widehat{AHO'}\) = \(\dfrac{1}{2}\) \(\widehat{OAO'}\) = \(\dfrac{1}{2}\) \(\widehat{XOY}\)
⇒ \(\widehat{ZOA}\) = \(\widehat{AHO'}\) (hai góc này ở vị trí so le trong)
⇒ OZ // O'Z' (đpcm)

A = -7 + (x - 1)^2
(x - 1)^2 > 0
=> A > -7
xét A = -7 khi x - 1 = 0
=> x = 1
vậy Min A = -7 khi x = 1
Ta có y O z ^ + x O z ^ = z O y ^ (cùng bằng 130°). Vậy tia Oz nằm giữa hai tia Ox và Oy.