Cho tam giác ABC vuông tại A. Góc C = 60 độ. Canh AB = \(\sqrt{192}\). Tính SABC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Xét ΔABC vuông tại A có
\(AC=AB\cdot\cot\widehat{C}\)
\(\Leftrightarrow AC=\sqrt{192}\cdot\cot60^0=8\left(cm\right)\)
Ta có: ΔABC vuông tại A(gt)
nên \(S_{ABC}=\dfrac{AB\cdot AC}{2}=\dfrac{8\sqrt{3}\cdot8}{2}=32\sqrt{3}\left(cm^2\right)\)

Vì tam giác ABC vuông ở A
=>AB^2+AC^2=BC^2
AB^+AC^2=100 (=6^2+8^2)
Xét tam giác ABC có
90 +60+C=180
C=30
Vì B>C
=>AB<AC(đ/lý.....)
=>AB=6

a: (SB;(ABC))=(SB;BA)=góc SBA
\(\tan SBA=\dfrac{SA}{AB}=\sqrt{6}\)
=>góc SBA=68 độ
b: (SA;(SBC))=(SA;SB)=góc ASB
tan ASB=AB/SA=1/căn 6
=>góc ASB=22 độ

Đáp án B.
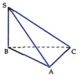
Ta có S B ⊥ ( A B C ) ⇒ B C là hình chiếu của SC trên mặt phẳng (ABC).
Suy ra S C , ( A B C ) ^ = S C , B C ^ = S C B ^ = 60 0
Do Δ A B C vuông tại A nên
S B = B C . tan S C B ^ = 2 a . tan 60 0 = 2 a 3 .
⇒ B C = A B 2 + A C 2 = a 2 + a 3 2 = 2 a .
Do Δ S B C vuông tại B nên
S B = B C . tan S C B ^ = 2 a . tan 60 0 = 2 a 3 .
Vậy
V S . A B C = 1 3 S B . S Δ A B C = 1 6 S B . A B . A C = 1 6 .2. 3 a . a . a 3 = a 3 (đvtt).


c b
AB^2+AC^2=BC^2
AC^2+ CĂN 192=4AC^2 (VÌ AC =1/2 BC)
SUY RA 3AC^2=CĂN 192
SUY RA AC^2=\(\frac{\sqrt{192}}{3}\)
SUY RA AC=