Question

[Hoàng Đức Long]

Cho hai loa là nguồn phát sóng âm $S_1, S_2$ phát âm cùng phương trình $u_{S1 }= u_{S2} = a\cos \omega t$ . Vận tốc sóng âm trong không khí là 330 (m/s). Một người đứng ở vị trí M cách $S_1$ 3 (m), cách $S_2$ 3,375 (m). Vậy tần số âm bé nhất, để ở M người đó không nghe được âm từ hai loa là bao nhiêu?

A. 420 (Hz)

B. 440 (Hz)

C. 460 (Hz)

D. 480 (Hz)

Answer 1

[Vũ Thành Nam]

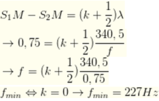
Đáp án B