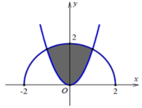
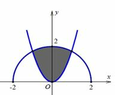
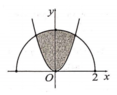
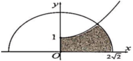
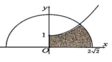
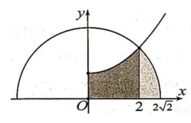
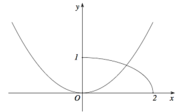
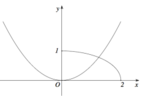
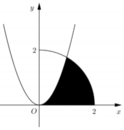
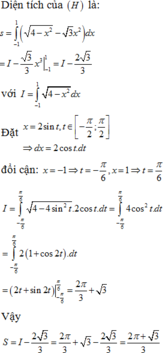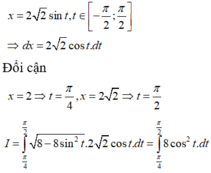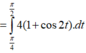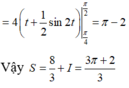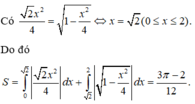Cho (H) là hình phẳng giới hạn bởi parabol với , nửa đường tròn và trục hoành, trục tung (phần tô đậm trong hình vẽ). Diện tích của (H) bằng
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Chọn D.
Hoành độ giao điểm của (P) và ( C) là nghiệm của 3 x 2 = 4 - x 2 <=> x = 1 hoặc x = -1
Khi đó, diện tích cần tính là H = 2x ( ∫ 0 1 4 - x 2 d x - ∫ 0 1 3 x 2 d x ) = 2 π + 3 3

Đáp án B.
Phương trình hoành độ giao điểm là:
3 x 2 = 4 − x 2 ⇒ 0 ≤ x ≤ 2 3 x 4 = 4 − x 2 ⇔ x = 1.
Dựa vào hình vẽ ta có:
S = ∫ 0 1 3 x 2 d x + ∫ 1 2 4 − x 2 d x = 3 x 3 3 1 0 + I 1 = 3 3 + I 1
Với I = ∫ 1 2 4 − x 2 d x , sử dụng CASIO
hoặc đặt x = 2 sin t ⇒ d x = 2 cos t d t
Đổi cận
x = 1 ⇒ t = π 6 x = 2 ⇒ t = π 2 ⇒ I 1 = ∫ π 6 π 2 4 − 4 sin 2 t . c o s tdt = ∫ π 6 π 2 2 1 + c o s 2 t d t = 2 t − sin 2 t π 2 π 6
⇒ I 1 = 1 6 4 π − 3 3 . Do đó S = 4 π − 3 6 .