Hình chóp SABC, đáy ABCD là hình bình hành; (α) là mặt phẳng chứa A và trung điểm M của SC, (α) // BD. Biết (α) chia SABCD thành 2 phần có thể tích V1, V2 (V1 là thể tích bé hơn). Tính
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1: Số mặt bên là 4
\(SAB;SAD;SBC;SCD\)
2: Số cạnh đáy là 4
AB,BC,CD,DA
3: SA và BC là hai đường thẳng chéo nhau
4: 4 đỉnh: A,B,C,D
5: Có 7 mặt: \(SAB;SAD;SBC;SCD;SAC;SBD;ABCD\)
6C

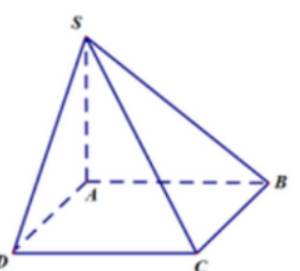
Hình chóp S.ABCD có các mặt bên là hình tam giác nên hình biểu diễn của nó cũng có các mặt bên là hình tam giác.
ABCD là hình bình hành nên hình biểu diễn của nó cũng là hình bình hành
Từ đó, ta vẽ được hình biểu diễn của hình chóp S.ABCD

Đáp án B
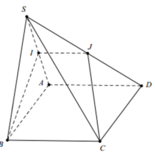
Do A D / / B C
Do đó \ I B C ∩ S A D = IJ ⇒ I J / / A D / / B C

Đáp án B
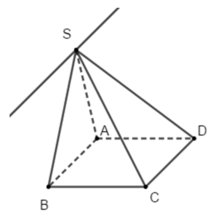
Ta có: AB ⊂ (SAB); CD ⊂ (SCD)
AB // CD (ABCD là hình bình hành)
S ∈ (SAB) ∩ (SCD)
Do đó giao tuyến của hai mặt phẳng (SAB) và (SCD) là đường thẳng đi qua S và song song với AB.
Vậy đáp án B đúng và C, D sai.
Đáp án A sai vì giao tuyến là đường thẳng, không phải điểm.
Chọn đáp án B.
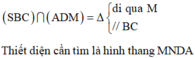
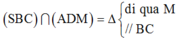
Đáp án B