Cho phân số M = n + 1 n (n ∈ ℤ ; n ≠ 0). Tìm n để A là phân số tối giản
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


không thể, vì để có phân số mới bằng phân số a/b thì m=n và n khác 0

có phân số a/b (a;b thuộc Z, b khác 0) và a/b = am/bn khi a = 0
VD :
0/b = 0.m/bn
\(\frac{a}{b}=\frac{a}{b}.\frac{m}{n}\Leftrightarrow\frac{a}{b}\left(1-\frac{m}{n}\right)=0\Leftrightarrow\orbr{\begin{cases}\frac{a}{b}=0\\\frac{m}{n}=1\end{cases}}\)
Do \(m\ne n\Rightarrow\frac{m}{n}\ne1\Rightarrow\frac{a}{b}=0\Rightarrow a=0\)
Vậy a=0, b là số nguyên khác 0

Chọn D.
Tính I = ∫ 1 2 3 d x x + 1 2 x + 3
Đặt t = 2 x + 3 ⇒ t 2 = 2 x + 3 ⇒ 2 t d t = 2 d x x = t 2 - 3 2 ⇒ d x = t d t x + 1 = t 2 - 1 2
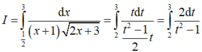
Vậy: m = 2, n = -1, T = 3.2 - 1 = 5.

a) B = 10 n 5 n − 3 = 10 n − 6 5 n − 3 + 6 5 n − 3 = 2. 5 n − 3 5 n − 3 + 6 5 n − 3 = 2 + 6 5 n − 3
B có giá trị nguyên khi 6 5 n − 3 có giá trị nguyên, tức là 6 ⋮ 5 n − 3 hay 5 n − 3 ∈ Ư ( 6 ) .
Ư ( 6 ) = ± 1 ; ± 2 ; ± 3 ; ± 6
Ta có bảng sau:
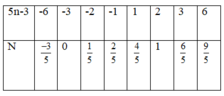
Dựa vào bảng ta thấy n ∈ 0 ; 1
b) B đạt giá trị lớn nhất khi 6 5 n − 3 đạt giá trị lớn nhất, tức là 5n-3 đạt giá trị nguyên dương nhỏ nhất, khi n=1. Khi đó GTLN của B là 5.

Ta có 8n+1=8(n+2)-8
=> 8 chia hết cho n+2
n nguyên => n+2 nguyên => n+2 \(\inƯ\left(8\right)=\left\{-8;-4;-2;-1;1;2;4;8\right\}\)
Ta có bảng
| n+2 | -8 | -4 | -2 | -1 | 1 | 2 | 4 | 8 |
| n | -10 | -6 | -4 | -3 | -1 | 0 | 2 | 6 |

Ta có: n + 9 là ước số của 4n + 22
=> 4n + 22 chia hết n + 9
<=> (4n + 36) - 14 chia hết n + 9
<=> 4.(n + 9) - 14 chia hết n + 9
=> 14 chia hết n + 9
=> n + 9 \(\in\) Ư(14) = { - 1;1;-2;2;-3;3;-4;4;-7;7-14;14}
=> n= { tự tính hộ nhé}
Ta có: n + 9 là ước số của 4n + 22
=> 4n + 22 chia hết n + 9
<=> (4n + 36) - 14 chia hết n + 9
<=> 4.(n + 9) - 14 chia hết n + 9
=> 14 chia hết n + 9
=> n + 9 $\in$∈ Ư(14) = { - 1;1;-2;2;-3;3;-4;4;-7;7-14;14}
=> n= { tự tính hộ nhé}
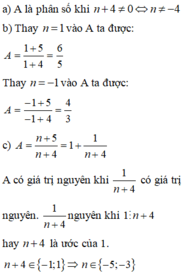

Để M = n + 1 n là phân số tối giản thì ƯCLN ( n +1,n) = 1
Gọi ƯCLN ( n + 1,n) = d => n + 1 ⋮ d; n ⋮ d
=> ( n + 1) – n ⋮ d=> 1 ⋮ d=> d = 1 với mọi n. Vậy với mọi n ∈ ℤ thì M = n + 1 n là phân số tối giản.