Trong không gian tọa độ Oxyz, cho đường thẳng và điểm . Hai điểm B, C di động trên đường thẳng d sao cho mặt phẳng vuông góc với . Gọi điểm B’ là hình chiếu vuông góc của điểm B lên đường thẳng AC. Biết quỹ tích các điểm B’ là một đường tròn cố định, tính bán kính r của đường tròn này.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C.
Đường thẳng d có véc tơ chỉ phương u → ( 2 ; 2 ; - 1 )
Gọi H(1+2t ;-1+2t ;-t) ∈ d là tọa độ hình chiếu vuông góc của A trên d.
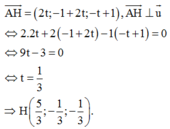
A’ đối xứng với A qua d ⇔ H là trung điểm của AA’
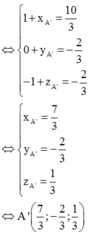

Thay lần lượt tọa độ các điểm vào phương trình đường thẳng ta thấy tọa độ của Q không thỏa mãn phương trình. Vậy điểm Q không thuộc đường thẳng d.
Chọn D

Đáp án D
Phương pháp:
Thay tọa độ các điểm vào phương trình đường thẳng và kiểm tra tọa độ đó có thỏa mãn phương trình hay không.
Cách giải
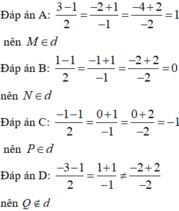

Chọn A
Vì A thuộc ![]() nên A (1+2t;1-t;-1+t).
nên A (1+2t;1-t;-1+t).
Vì B thuộc ![]() nên B (-2+3t';-1+t';2+2t').
nên B (-2+3t';-1+t';2+2t').

Thay vào (3) ta được t=1, t'=2 thỏa mãn.

Đáp án C
HD: Gọi H(1+2t;-1+t;2-t) là hình chiếu của A trên d
![]()
![]()
Suy ra H(3;0;1), phương trình đường thẳng AH là
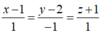
![]()

Đáp án C
Gọi B 2 + t ; - 1 - t ; 1 + t A B ¯ = 1 + t ; - t ; t - 2 . Cho A B ¯ . u d ¯ = 0 ⇔ t + 1 - 4 t - 2 t + 4 = 0 ⇔ t = 1 ⇒ A B ¯ = 2 ; - 1 ; - 1
Khi đó d : x - 1 2 = y + 1 - 1 = z - 3 - 1 .

Chọn C
Đường thẳng d đi qua điểm M(-2;1;3) và có vectơ chỉ phương ![]()

Chọn C
Đường thẳng d đi qua điểm M(-2;1;3) và có vectơ chỉ phương ![]()


Chọn đáp án B
trên H là hình chiếu của O lên đường thẳng d.
Suy ra điểm B’ thuộc đường tròn đường kính AK, đường tròn này vẽ trong mặt phẳng (A,d)
Cách 2: Vì B’ là hình chiếu của B lên AC nên A B ' ⊥ O B ' , suy ra B’ thuộc mặt cầu (S), đường kính AO.