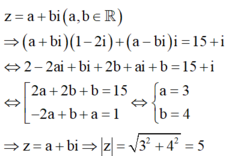Tìm môđun của số phức z=a+bi (a,bÎR) thỏa mãn z - 4 = 1 + i z - 4 + 3 z i
A. z = 1
B. z = 1 2
C. z = 2
D. z = 4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

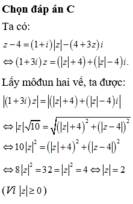

\(\Leftrightarrow z\left(3i+1\right)=\left(\left|z\right|-4\right)i+\left|z\right|+4\)
Lấy module 2 vế:
\(\Rightarrow\left|z\right|.\sqrt{10}=\sqrt{\left(\left|z\right|-4\right)^2+\left(\left|z\right|+4\right)^2}\)
Đặt \(\left|z\right|=x>0\Rightarrow x\sqrt{10}=\sqrt{\left(x-4\right)^2+\left(x+4\right)^2}\)
\(\Leftrightarrow10x^2=2x^2+32\)
\(\Leftrightarrow x^2=4\)
\(\Rightarrow x=2\)
Vậy \(\left|z\right|=2\)

Đáp án A
Phương pháp
Gọi ![]()
Sử dụng định nghĩa hai số phức bằng nhau.
Cách giải