Tính tổng: a) 1- 2+3 - 4+5 - 6 +...- 2016; b) 1+(- 6)+2+(-7)+3+(-8) +... +15+(-20)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
26 tháng 3 2019
Đúng(0)
Những câu hỏi liên quan
TT
1
28 tháng 1 2018
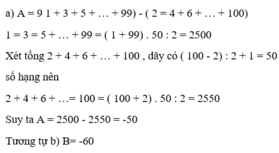
A = (1-2-3+4)+(5-6-7+8)+.....+(2013-2014-2015+2016)
= 0+0+.....+0
= 0
Tk mk nha
NM
4
14 tháng 1 2018
1, có từ 1đến 100 có 100 số hạng .Chia thành 50 nhóm .Mỗi nhóm co 2 số hạng
Suy ra A= [1+(-2)]+[3+(-4)]+......+[99+(-100)]
A= (-1)+(-1)+.... +(-1)
A= (-1).50=(-50)
2,A=(1-2)+(3-4)+.....+(2015-2016)
A=(-1)+(-1)+....+(-1)
A có 2016 số hạng .Chia thành 1008 nhóm .Mỗi nhóm co 2 số hạng và có tổng =(-1)
A=(-1).1008=(-1008)
LV
14 tháng 1 2018
\(A=\left(1+3+...+99\right)-\left(2+4+...+100\right)\)
\(A=\left(\left(1+99\right)\cdot\frac{50}{2}\right)-\left(\left(2+100\right)\cdot\frac{50}{2}\right)\)
\(A=2500-2550=-50\)
Đúng ko ta lâu rồi ko làm.
\(A=\left(\left(1+99\right)\cdot\frac{50}{2}\right)-\left(\left(2+100\right)\cdot\frac{50}{2}\right)\)
S
14 tháng 2 2020
\(A=\left[1+\left(-2\right)\right]+\left[3+\left(-4\right)\right]+....+\left[2013+\left(-2014\right)+2015\right]\)
\(A=\left(-1\right)+\left(-1\right)+....+\left(-1\right)+2015\left(\text{1007 số hạng }\left(-1\right)\right)=1008\)
NB
1
12 tháng 12 2016
a, số số hạng là: (2018-2)/2+1=1009(số hạng)
tb+ của dãy là: (2018+2)/2=1010
tổng của dãy là:1009*1010=.......
a cho e 1* nhé
NM
3
TD
17 tháng 1 2017
\(S=1-2+3-4+5-6+...+2015-2016\)
\(S=\left(1-2\right)+\left(3-4\right)+\left(5-6\right)+...+\left(2015-2016\right)\)
\(S=\left(-1\right)+\left(-1\right)+\left(-1\right)+...+\left(-1\right)\)
Dãy S có 2016 số =>Có 1008 cặp -1.
\(S=\left(-1\right).1008\)
\(\Rightarrow\)\(S=-1008\)
Tk mk nhé(nếu đúng)!Thank you!
17 tháng 1 2017
S= (1-2)+(3-4)+...+(2015-2016)(có 1008 ch/số)
=-1+(-1)+...+(-1)(có 1008 ch/s 1 )
=-1.2008
=-1
LF
2
8 tháng 5 2016
S = (1+3+5+...+2015) - (2+4+6+...+2016)
S = 1016064 - 1017072
S = -1008
Chúc bạn học tốt !!!!
3 tháng 5 2019
A = \(\frac{5}{2.4}+\frac{5}{4.6}+\frac{5}{6.8}+...+\frac{5}{2014.2016}\)
A = \(5.\frac{1}{2}.\left(\frac{2}{2.4}+\frac{2}{4.6}+\frac{2}{6.8}+...+\frac{2}{2014.2016}\right)\)
A = \(\frac{5}{2}.\left(\frac{1}{2}-\frac{1}{4}+\frac{1}{4}-\frac{1}{6}+\frac{1}{6}-\frac{1}{8}+...+\frac{1}{2014}-\frac{1}{2016}\right)\)
A = \(\frac{5}{2}.\left(\frac{1}{2}-\frac{1}{2016}\right)\)
A = \(\frac{5}{2}.\frac{1007}{2016}=\frac{5035}{4032}\)
KN
3 tháng 5 2019
\(A=\frac{5}{2.4}+\frac{5}{4.6}+\frac{5}{6.8}+...+\frac{5}{2014.2016}\)
\(\Rightarrow\frac{2}{5}A=\frac{2}{2.4}+\frac{2}{4.6}+\frac{2}{6.8}+...+\frac{2}{2014.2016}\)
\(\Rightarrow\frac{2}{5}A=\frac{1}{2}-\frac{1}{4}+\frac{1}{4}-\frac{1}{6}+\frac{1}{6}-\frac{1}{8}+...+\frac{1}{2014}-\frac{1}{2016}\)
\(\Rightarrow\frac{2}{5}A=\frac{1}{2}-\frac{1}{2016}\)
\(\Rightarrow\frac{2}{5}A=\frac{1008}{2016}-\frac{1}{2016}\)
\(\Rightarrow\frac{2}{5}A=\frac{1007}{2016}\)
\(\Rightarrow A=\frac{1007}{2016}\div\frac{2}{5}\)
\(\Rightarrow A=\frac{1007}{2016}\times\frac{5}{2}\)
\(\Rightarrow A=\frac{5035}{4032}\)