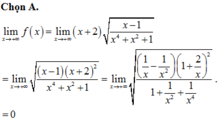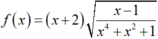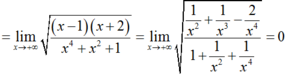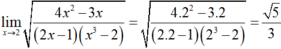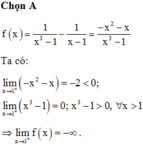Cho hàm số . Chọn kết quả đúng của :
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(\lim\limits_{x\rightarrow+\infty}f\left(x\right)=\lim\limits_{x\rightarrow+\infty}\dfrac{1+3x}{\sqrt{2x^2+3}}\)
\(=\lim\limits_{x\rightarrow+\infty}\dfrac{3+\dfrac{1}{x}}{\sqrt{2+\dfrac{3}{x^2}}}=\dfrac{3+0}{\sqrt{2+0}}=\dfrac{3}{\sqrt{2}}\)
\(=\dfrac{3\sqrt{2}}{2}\)

Chọn A.
Đặt u = ln x + x 2 + 1 , d v = d x ta được
F(x)=x ln x + x 2 + 1 - x 2 + 1 + C
Vì F(0) = 1 nên C = 2
Vậy ![]()

Chọn A
1 x 3 − 1 − 1 x − 1 = 1 ( x − 1 ) . ( x 2 + x + 1 ) − 1 x − 1 = 1 − ( x 2 + x + 1 ) ( x − 1 ) . ( x 2 + x + 1 ) = − x 2 − x ( x − 1 ) . ( x 2 + x + 1 ) = − x 2 − x x 3 − 1
lim x → 1 + f x = lim x → 1 + − x 2 − x x 3 − 1
lim x → 1 + − x 2 − x = − 2
khi x → 1 + ⇒ x > 1 ⇒ x 3 − 1 > 0
vậy lim x → 1 + f x = − ∞