Question

[Pham Trong Bach]

Cho phương trình 2 cos 2 x cos 2 x − cos 2018 π 2 x = cos 4 x − 1 . Tính tổng tất cả các nghiệm thực dương của phương trình.

A. π

B. 1010 π

C. 1001 π

D. 1100 π

Answer 1

[Cao Minh Tâm]

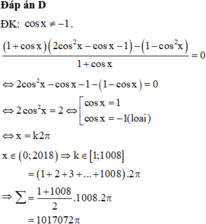
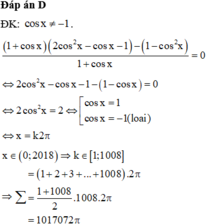
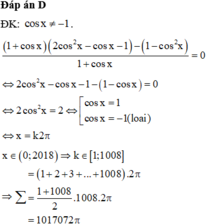
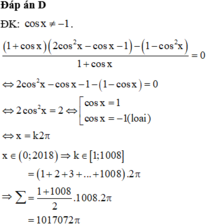
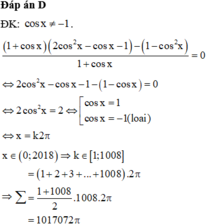
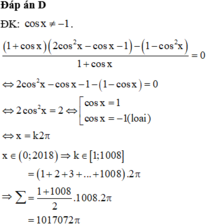
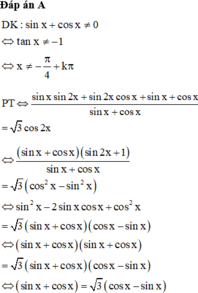
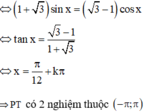
Đáp án B.

Điều kiện:  x ≠ 0   .

Ta có  2 cos 2 x cos 2 x − cos 2018 π 2 x = cos 4 x − 1

⇔ 2 cos 2 2 x − 2 cos 2 x . cos 2018 π 2 x = cos 4 x − 1

⇔ cos 4 x + 1 − 2 cos 2 x . cos 2018 π 2 x = cos 4 x − 1

⇔ cos 2 x . cos 2018 π 2 x = 1  

ta có  cos 2 x . cos 2018 π 2 x ≤ 1  

do đó  cos 2 x . cos 2018 π 2 x = 1 ⇔ cos 2 x = 1 cos 2018 π 2 x = 1 hoặc  cos 2 x = − 1 cos 2018 π 2 x = − 1

cos 2 x = 1 cos 2018 π 2 x = 1 ⇔ x = k π x = 1009 π l k , l ∈ ℤ

⇒ k l = 1009 ⇒ k = 1009 l = 1 hoặc  k = − 1009 l = − 1 hoặc k = 1 l = 1009 hoặc  k = − 1 l = − 1009

Trong trường hợp này tổng các nghiệm dương của phương trình bằng  1010 π

cos 2 x = − 1 cos 2018 π 2 x = − 1 ⇔ x = π 2 + k π x = 2018 π 1 + 2 l k , l ∈ ℤ

⇒ 1 2 + k = 2018 1 + 2 l ⇒ 1 + 2 k 1 + 2 l = 2.2018 (*)

Vế trái của (*) là số lẻ, vế phải của (*) là số chẵn. Do đó không có giá trị nguyên nào của k, l thỏa mãn (*).

* Tóm lại: Tổng các nghiệm dương của phương trình bằng 1010π.