Gọi lần lượt là công thoát êlêctron khỏi đồng, kẽm, canxi. Giới hạn quang điện của đồng, kẽm, can xi lần lượt là 0,3 µm, 0,35 µm, 0,45 µm. Kết luận nào sau đây đúng?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1.
\(\dfrac{V_{SAMC}}{V_{SABC}}=\dfrac{SM}{SB}\)
Theo hệ thức lượng: \(SA^2=SM.SB\Rightarrow SM=\dfrac{SA^2}{SB}\)
\(\Rightarrow\dfrac{SM}{SB}=\left(\dfrac{SA}{SB}\right)^2\)
\(\Rightarrow V_{SAMC}=\left(\dfrac{SA}{SB}\right)^2.V\)
2.
Ta có: \(\dfrac{V_{SAMN}}{V_{SABC}}=\dfrac{SN}{SC}.\dfrac{SM}{SB}\)
Theo c/m câu a ta có \(\dfrac{SM}{SB}=\left(\dfrac{SA}{SB}\right)^2\)
Tương tự áp dụng hệ thức lượng cho tam giác vuông SAC:
\(SA^2=SN.SC\Rightarrow SN=\dfrac{SA^2}{SC}\Rightarrow\dfrac{SN}{SC}=\left(\dfrac{SA}{SC}\right)^2\)
\(\Rightarrow V_{SAMN}=\left(\dfrac{SA}{SB}\right)^2.\left(\dfrac{SA}{SC}\right)^2.V\)

Ta có; AA1=AB/2
AA2=AB/22
....
AA2017=AB/22017
=22017/22017
=1cm
Độ dài của đoạn AA1 là AB:2
Độ dài của đoạn AA2 là AA1:2 = AB:4
....
Độ dài của đoạn AA2017 là AB/(2^2017) = 1cm

Chọn B
Gọi A (0; 0; a). Đường thẳng AB qua A và vuông góc với (α) có phương trình 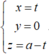
B là hình chiếu của A lên (α) nên tọa độ B thỏa mãn hệ
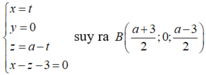
Tam giác MAB cân tại M nên
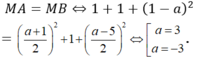
· Nếu a = -3 thì tọa độ A (0; 0; -3) và B (0; 0; -3) trùng nhau, loại.
· Nếu a = 3 thì tọa độ A (0; 0; 3), B (3; 0; 0)
Diện tích tam giác MAB bằng
![]()

Ta có:
A:3=c=>A=3c
B:5=c=>B=5c
A+B=364,8
=>3c+5c=364,8
8c=364,8
c=45,6
- A=3c=45,6.3=136,8
- B=5c=45,6.5=228
theo bài ( A+B) gấp 8 lần C nên ta có tổng số phần là A+B+C=3+5+1=9
A=365,8:11 .3
B VÀ C LÀM TƯƠNG TỰ A

a: Xét tứ giác ABOC có
\(\widehat{ABO}+\widehat{ACO}=180^0\)
Do đó: ABOC là tứ giác nội tiếp
+ Công thoát tỉ lệ nghịch với giới hạn quang điện, do vậy với λ 1 > λ 2 > λ 3 → A 1 > A 2 > A 3 → Đáp án B