Gọi (P) là mặt phẳng đi qua điểm cắt các tia Ox, Oy, Oz lần lượt tại A, B, C sao cho biểu thức có giá trị nhỏ nhất. Mặt phẳng (P) đi qua điểm nào dưới đây?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Có duy nhất một đường thẳng đi qua M song song với d
b) Nếu một đường thẳng đi qua M và song song với d thì đường thẳng đó có thuộc mặt phẳng (P) vì hai đường thẳng song song đồng phẳng

a) Ta có: AD // BC (ABCD là hình bình hành)
Mà AD thuộc (AFD), BC thuộc (BEC)
Nên (AFD) // (BEC)
b) Trong (ABEF) kẻ đường thẳng d qua M // AF
Ta có: d cắt AB tại I, d cắt EF tại J (1)
Trong (ABCD) có I thuộc (P) mà (P) // (AFD)
Suy ra từ I kẻ IH // AD (2)
(1)(2) suy ra (IJH) trùng (P) và // (AFD)
Ta có: (P) cắt AC tại N mà AC thuộc (ABCD), IH thuộc (P) và (ABCD)
Suy ra: IH cắt AC tại N
Ta có các hình bình hành IBCH, IBEJ
Gọi O là trung điểm của AB
Có M là trọng tâm △ABE
Suy ra: \(\dfrac{MO}{ME}=\dfrac{1}{2}\).
Ta có: AB // CD suy ra: AI // CH
Định lí Ta-lét: \(\dfrac{AN}{NC}=\dfrac{AI}{CH}\)
mà CH = IB (IBCH là hình bình hành)
Suy ra: \(\dfrac{AN}{NC}=\dfrac{AI}{IB}\)
Ta có: AB // EF nên OI // EJ
Do đó: \(\dfrac{OI}{EJ}=\dfrac{MO}{ME}=\dfrac{1}{2}\)
Mà EJ = IB (IBEJ là hình bình hành)
Suy ra: \(\dfrac{OI}{IB}=\dfrac{1}{2}\) hay IB = 2OI
Ta có: \(\dfrac{AN}{NC}=\dfrac{AI}{IB}=\dfrac{AO+OI}{2OI}\)
Mà OA = OB (O là trung điểm AB)
Nên \(\dfrac{AN}{NC}=2\).

Định chụp hình cơ cơ mà khá khó nhìn nên thoi đánh máy, bạn cố hiểu nhé
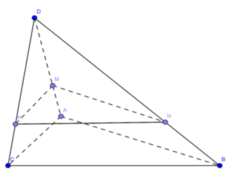
Từ H kẻ đường thẳng song song với ME cắt BC ở K
Từ K kẻ đường thẳng song song với EN cắt CD ở I
Nối I với H ta được mp (P) cần tìm
\(\left\{{}\begin{matrix}K\in HK\subset\left(HKI\right);K\in BC\subset\left(BCD\right)\\I\in KI\subset\left(HKI\right);I\in CD\subset\left(BCD\right)\end{matrix}\right.\Rightarrow\left(HKI\right)\cap\left(BCD\right)=KI\Rightarrow\left(P\right)\cap\left(BCD\right)=KI\)
Ta co \(\left\{{}\begin{matrix}H\in HK\subset\left(HKI\right);H\in AB\subset\left(ABD\right)\\KI//AB\end{matrix}\right.\)
=> Giao tuyen cua (P) va (ABD) la duong thang ua H va song song voi BD

Đáp án B.
Phương pháp:
Mặt phẳng α nhận i → 1 ; 0 ; 0 , O M → = 1 ; − 1 ; 2 là cặp vecto chỉ phương ⇒ n → = i → ; O M → là một vecto pháp tuyến của α
Cách giải:
α là mặt phẳng đi qua M 1 ; − 1 ; 2 và chứa trục Ox ⇒ α nhận i → 1 ; 0 ; 0 , O M → = 1 ; − 1 ; 2 là cặp vecto chỉ phương ⇒ n → = i → ; O M → = 0 ; − 2 ; − 1 là một vecto pháp tuyến của α .
α : 0. x − 0 − 2. y − 0 − 1 z − 0 = 0 ⇔ 2 y + z = 0
Dễ dàng kiểm tra N 2 ; 2 ; − 4 ∈ α

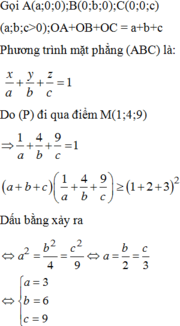


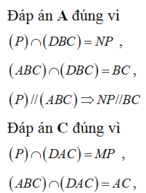


Đáp án D.
Do (P) cắt Ox; Oy; Oz lần luợt tại A,B, C.
Gọi A a ; 0 ; 0 ; B 0 ; b ; 0 ; C 0 ; 0 ; c a ; b ; c > 0
Khi đó
A B C : x a + y b + z c = 1 ; O A + O B + O C = a + b + c
(P) qua M 9 ; 1 ; 4 ⇒ 9 a + 1 b + 4 c = 1
Áp dụng BĐT: x + y + z a 2 x + b 2 y + c 2 z ≥ a + b + c 2
ta có: a + b + c 9 a + 1 b + 4 c ≥ 3 + 1 + 2 2 = 36
Do đó O A + O B + O C = a + b + c ≥ 36
Dấu bằng xảy ra
⇔ 9 a 2 = 1 b 2 = 4 c 2 9 a + 1 b + 4 c = 1 ⇔ a = 18 ; b = 6 ; c = 12 ⇒ A B C : x 18 + y 6 + z 12 = 1.