Trong không gian với hệ tọa độ Oxyz, cho điểm A 2 ; 3 ; 0 , B 0 ; − 2 ; 0 , M 6 5 ; − 2 ; 2 và đường thẳng d : x = t y = 0 z = 2 − t . Điểm C thuộc d sao cho chu vi tam giác ABC là nhỏ nhất thì độ dài CM bằng
A. 2 3 .
B.4
C.2
D. 2 6 5 .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án C.
Gọi điểm H là hình chiếu của A 4 ; 1 ; − 2 trên mặt phẳng O x z , khi đó H 4 ; 0 ; − 2 .
Điểm A' đối xứng với A 4 ; 1 ; − 2 qua mặt phẳng O x z nên H 4 ; 0 ; − 2 là trung điểm AA' . Khi đó A ' 2 x H − x A ; 2 y H − y A ; 2 z H − z A → A ' 4 ; − 1 ; − 2
. Tìm tọa độ điểm A.
Đáp án A
Dễ thấy tọa độ trung điểm của đoạn thẳng AB là điểm.
Đáp án A
Dễ thấy tọa độ trung điểm của đoạn thẳng AB là điểm
Đáp án A
Ta có xA' = 2xO-xA = 3; yA' = 2yO-yA = -2; zA' = 2zO-zA=1. Vậy A'(3;-2;1).
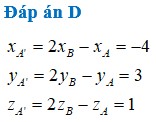
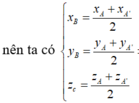
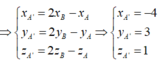
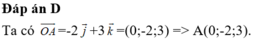
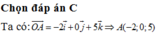
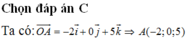
Đáp án C
Do AB có độ dài không đổi nên chu vi tam giác ABC nhỏ nhất khi tổng A C + B C nhỏ nhất.
Do
C ∈ d ⇒ C t ; 0 ; 2 − t ⇒ A C = 2 t − 2 2 + 9 B C = t 2 + 2 − t 2 + 2 = 2 1 − t 2 + 4
Suy ra A C + B C = 2 t − 2 2 2 + 9 + 2 − 2 t 2 + 4 .
Đặt u → = 2 t − 2 2 ; 3 và v → = 2 − 2 t ; 2 . Áp dụng bất đẳng thức u → + v → ≥ u → + v → , dấu “=” xảy ra khi và chỉ khi u → , v → cùng hướng ta được:
2 t − 2 2 2 + 9 + 2 − 2 t 2 + 4 ≥ − 2 2 + 5 2 = 27
Dấu “=” xảy ra ⇔ 2 t − 2 2 2 − 2 t = 3 2 ⇔ t − 2 1 − t = 3 2 ⇔ t = 7 5 . Suy ra C 7 5 ; 0 ; 3 5 .
Vậy C M = 7 5 − 6 5 2 + 0 + 2 2 + 3 5 − 2 2 = 2