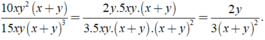Rút gọn phân thức : x 4 - y 4 y 3 - x 3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
8 tháng 9 2017
Đúng(0)
Những câu hỏi liên quan
LT
0
2G
1
DE
14 tháng 8 2019
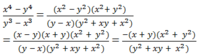
\(\frac{x^4-y^4}{y^3-x^3}\)
\(=\frac{\left(x^2+y^2\right)\left(x^2-y^2\right)}{\left(y-x\right)\left(y^2+xy+x^2\right)}\)
\(=\frac{\left(x^2+y^2\right)\left(x+y\right)\left(x-y\right)}{\left(y-x\right)\left(y^2+xy+x^2\right)}\)
\(=-\frac{\left(x^2+y^2\right)\left(x+y\right)\left(x-y\right)}{\left(x-y\right)\left(x^2+xy+y^2\right)}\)
\(=-\frac{\left(x^2+y^2\right)\left(x+y\right)}{x^2+xy+y^2}\)
HP
21 tháng 11 2021
1. \(\dfrac{x^3-4x^2+4x}{x^2-4}=\dfrac{x\left(x^2-4x+4\right)}{\left(x+2\right)\left(x-2\right)}=\dfrac{x\left(x-2\right)^2}{\left(x+2\right)\left(x-2\right)}=\dfrac{x\left(x-2\right)}{x+2}\)
20 tháng 10 2021
\(a,P=x^2-16-x^2+8x-16=8x-32\\ b,=3x^2-6xy+3y^2-2x^2-4xy-2y^2-x^2+y^2\\ =2y^2-10xy=2\cdot9-10\left(-3\right)\cdot2=78\)
PB
1
28 tháng 9 2017
\(\left(x-y\right)\left(x+y\right)\left(x^2+y^2\right)\left(x^4+y^4\right)\)
\(=\left(x^2-y^2\right)\left(x^2+y^2\right)\left(x^4+y^4\right)\)
\(=\left(x^4-y^4\right)\left(x^4+y^4\right)\)
\(=x^8-y^8\)
3 tháng 12 2016
A) X4 - y4 / y3 -x3 = (x2) 2 - (y2 )2 / (y-x)(y^2+xy+x^2)= (x^2-y^2)(x^2+y^2) / (y-x)(y^2+xy+x^2)=-(x-y)(x+y)(x^2+y^2) / (x-y)(x^2+xy+y^2)= - (x+y)(x^2+y^2) / x^2 + xy + y^2
3 tháng 12 2016
Câu b, bạn nhóm các hạng tử vào vs nhau sẽ xuất hiện nhân tử chung rồi rút gọn đi là ok. Nhóm 2x^3 vs -2x, x^2 vs cộng 1 thì đặt dấu trừ ra ngoài.. Bên dưới nhóm x^3 vs -x,2x^2 vs -2
DQ
1
25 tháng 11 2019
\(\frac{y^3-x^3}{x^4-y^4}=\frac{\left(y-x\right)\left(y^2+xy+x^2\right)}{\left(x^2-y^2\right)\left(x^2+y^2\right)}=\frac{-\left(x-y\right)\left(y^2+xy+x^2\right)}{\left(x-y\right)\left(x+y\right)\left(x^2+y^2\right)}=\frac{-\left(y^2+xy+x^2\right)}{\left(x+y\right)\left(x^2+y^2\right)}\)
Y
29 tháng 6 2023
\(1,\left(x+y\right)^2-\left(x-y\right)^2=\left[\left(x+y\right)-\left(x-y\right)\right]\left[\left(x+y\right)+\left(x-y\right)\right]=\left(x+y-x+y\right)\left(x+y+x-y\right)=2y.2x=4xy\)
\(2,\left(x+y\right)^3-\left(x-y\right)^3-2y^3\)
\(=x^3+3x^2y+3xy^2+y^3-x^3+3x^2y-3xy^2+y^3-2y^3\)
\(=6x^2y\)
\(3,\left(x+y\right)^2-2\left(x+y\right)\left(x-y\right)+\left(x-y\right)^2\\ =\left[\left(x+y\right)-\left(x-y\right)\right]^2\\ =\left(x+y-x+y\right)^2\\ =4y^2\)
\(4,\left(2x+3\right)^2-2\left(2x+3\right)\left(2x+5\right)+\left(2x+5\right)^2\\ =\left[\left(2x+3\right)-\left(2x+5\right)\right]^2\\ =\left(2x+3-2x-5\right)^2\\ =\left(-2\right)^2\\ =4\)
\(5,9^8.2^8-\left(18^4+1\right)\left(18^4-1\right)\\ =18^8-\left[\left(18^4\right)^2-1\right]\\ =18^8-18^8+1\\ =1\)
29 tháng 6 2023
1: =x^2+2xy+y^2-x^2+2xy-y^2=4xy
2: =x^3+3x^2y+3xy^2+y^3-x^3+3x^2y-3xy^2+y^3-2y^3
=6x^2y
3: =(x+y-x+y)^2=(2y)^2=4y^2
4: =(2x+3-2x-5)^2=(-2)^2=4
5: =18^8-18^8+1=1
PT
1
