em hãy cho biết tên hàm tìm giá trị nhỏ nhất và cú pháp của hàm tìm giá trị nhỏ nhất
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Em hãy nêu cú pháp của hàm tính tổng tính trung bình cộng xác định giá trị lớn nhất giá trị nhỏ nhất



tổng trung bình
AVERAGE(A,B,C...)
GIÁ TRỊ LỚN NHẤT
MAX(A,B,C..)
GIÁ TRỊ NHỎ NHẤT
MIN(A,B,C...)
😅😄

Câu 1:
$y=-2x^2+4x+3=5-2(x^2-2x+1)=5-2(x-1)^2$
Vì $(x-1)^2\geq 0$ với mọi $x\in\mathbb{R}$ nên $y=5-2(x-1)^2\leq 5$
Vậy $y_{\max}=5$ khi $x=1$
Hàm số không có min.
Câu 2:
Hàm số $y$ có $a=-3<0; b=2, c=1$ nên đths có trục đối xứng $x=\frac{-b}{2a}=\frac{1}{3}$
Lập BTT ta thấy hàm số đồng biến trên $(-\infty; \frac{1}{3})$ và nghịch biến trên $(\frac{1}{3}; +\infty)$
Với $x\in (1;3)$ thì hàm luôn nghịch biến
$\Rightarrow f(3)< y< f(1)$ với mọi $x\in (1;3)$
$\Rightarrow$ hàm không có min, max.

các kí hiệu
cộng +
trừ -
nhân *
chia /
các bước nhập công thức
di chuyển con trỏ chuột và chon một ô
gõ dấu "=" và công thức
các bước nhập hàm
di chuyển con trỏ chuột và chon một ô
gõ dấu"=" và nhập hàm và địa chỉ ô tính
hàm SUM tính tổng
hàm AVERAGE là tính trung bình cộng
Max gtr lớn nhất
MIN gtr nhỏ nhất

1. Không dịch được đề
2.
\(-1\le cos2x\le1\Rightarrow1\le y\le3\)
3.
a. \(-2\le2sinx\le2\Rightarrow-1\le y\le3\)
\(y_{min}=-1\) khi \(sinx=-1\Rightarrow x=-\dfrac{\pi}{2}+k2\pi\)
\(y_{max}=3\) khi \(sinx=1\Rightarrow x=\dfrac{\pi}{2}+k2\pi\)
b.
\(0\le cos^2x\le1\Rightarrow-1\le y\le2\)
\(y_{min}=-1\) khi \(cos^2x=1\Rightarrow x=k\pi\)
\(y_{max}=2\) khi \(cosx=0\Rightarrow x=\dfrac{\pi}{2}+k\pi\)
4.
\(y=\left(tanx-1\right)^2+2\ge2\)
\(y_{min}=2\) khi \(tanx=1\Rightarrow x=\dfrac{\pi}{4}+k\pi\)

Hàm số có giá trị nhỏ nhất ⇔ y nhỏ nhất.
Dựa vào đồ thị nhận thấy cả ba hàm số đạt y nhỏ nhất tại điểm O(0; 0).
Vậy ba hàm số trên đều đạt giá trị nhỏ nhất tại x = 0.

Đáp án A.
Điều kiện x ∈ ℝ
y = cos x + cos x − π 3 = cos x + cos x . cos π 3 + sin x . sin π 3 = cos x + 1 2 cos x + 3 2 sin x
= 3 2 cos x + 3 2 sin x
Cách 1: y = 3 3 2 cos x + 1 2 sin x = 3 sin x + π 3 Suy ra − 3 ≤ y ≤ 3
Vậy m = − 3 ; M = 3 và do đó M 2 + m 2 = 6
Cách 2:
Áp dụng bất đẳng thức Bunyakovsky ta có:
3 2 cos x + 3 2 sin x 2 ≤ 3 2 2 + 3 2 2 cos x 2 + sin x 2
⇔ 3 2 cos x + 3 2 sin x 2 ≤ 3 ⇔ − 3 ≤ y ≤ 3
⇒ M = 3 khi 2 3 cos x = 2 3 sin x 3 2 cos x + 3 2 sin x = 3
Tương tự ta có m = − 3 khi 2 3 cos x = 2 3 sin x 3 2 cos x + 3 2 sin x = − 3
⇒ M 2 + m 2 = 3 2 + − 3 2 = 6
Vậy ta chọn A.

Tham khảo
y = 4sin √ x ( đk x ≥ 0 )
ta thấy: -1 ≤ sin √ x ≤ 1
<=> -4 ≤ 4sin √ x ≤ 4
<=> -4 ≤ y ≤ 4
max y = 4
dấu "=" xảy ra <=> sin √ x = 1
<=> √ x = pi/2 +2kpi
<=> x = (pi/2 +2kpi )^2
min y = -4
dấu "=" xảy ra <=> sin √ x = -1
<=> √ x = -pi/2 +2kpi
<=> x = (-pi/2 +2kpi)^2
a. \(y=2cos\left(x+\dfrac{\pi}{3}\right)+3\)
Ta có: \(-1\le cos\alpha\le1\)
\(\Leftrightarrow-2\le2cos\alpha\le2\)
\(\Leftrightarrow-2+3\le2cos\alpha+3\le2+3\)
\(\Leftrightarrow1\le2cos\alpha+3\le5\)
Vậy y đạt GTNN ymin=1 khi \(\left[{}\begin{matrix}x=\dfrac{2}{3}\pi+k2\pi\\x=\dfrac{-4}{3}\pi+k2\pi\end{matrix}\right.\) và y đạt GTLN khi ymax=5 khi \(x=-\dfrac{\pi}{3}+k2\pi\)
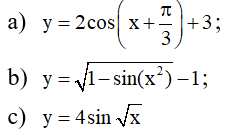
tên hàm tính giá trị nhỏ nhất là MIN.