Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
\(\dfrac{A}{2}+\dfrac{B}{2}=\dfrac{\pi}{2}-\dfrac{C}{2}\Rightarrow tan\left(\dfrac{A}{2}+\dfrac{B}{2}\right)=tan\left(\dfrac{\pi}{2}-\dfrac{C}{2}\right)\)
\(\Rightarrow\dfrac{tan\dfrac{A}{2}+tan\dfrac{B}{2}}{1-tan\dfrac{A}{2}tan\dfrac{B}{2}}=cot\dfrac{C}{2}=\dfrac{1}{tan\dfrac{C}{2}}\)
\(\Rightarrow tan\dfrac{A}{2}.tan\dfrac{C}{2}+tan\dfrac{B}{2}tan\dfrac{C}{2}=1-tan\dfrac{A}{2}tan\dfrac{B}{2}\)
\(\Rightarrow tan\dfrac{A}{2}tan\dfrac{B}{2}+tan\dfrac{B}{2}tan\dfrac{C}{2}+tan\dfrac{C}{2}tan\dfrac{A}{2}=1\)
Ta có:
\(tan\dfrac{A}{2}+tan\dfrac{B}{2}+tan\dfrac{C}{2}\ge\sqrt{3\left(tan\dfrac{A}{2}tan\dfrac{B}{2}+tan\dfrac{B}{2}tan\dfrac{C}{2}+tan\dfrac{C}{2}tan\dfrac{A}{2}\right)}=\sqrt{3}\)
Dấu "=" xảy ra khi và chỉ khi \(A=B=C\) hay tam giác ABC đều
a) Theo hệ thức đường cao trong tam giác vuông ta có:
\(AH^2=BH\cdot CH\Rightarrow CH=\dfrac{AH^2}{BH}=\dfrac{4^2}{2}=8\left(cm\right)\)
b) Áp dụng hệ thức cạnh góc vuông và hình chiếu ta có:
\(AC^2=BC\cdot CH\Rightarrow AC=\sqrt{\left(BH+CH\right)\cdot CH}=\sqrt{\left(8+2\right)\cdot8}=4\sqrt{5}\left(cm\right)\)
\(AB^2=BC\cdot BH\Rightarrow AB=\sqrt{\left(8+2\right)\cdot2}=2\sqrt{5}cm\)
Ta có:
\(tanB=\dfrac{AC}{BC}=\dfrac{4\sqrt{5}}{2\sqrt{5}}=2\)
A B C M N I
a) tam giác ABN và tam giác ABC chung chiều cao hạ từ B xuống AC ; đáy AN = 1/3 đáy AC
=> S(ABN) = 1/3 xS(ABC)
Tam giác ACM và ACB có chung chiều cao hạ từ C xuống AB ; đáy AM = 1/3 đáy AB
=> S(AMC) = 1/3 x S(ABC)
=> S(AMC) = S(ANB) Vì cùng bằng 1/3 S(ABC)
b) Ta có: S(AMC) = S(CNI) + S(AMIN)
S(ANB) = S(BMI) + S(AMIN)
Mà S(AMC) = S(ANB) nên S(CNI) = S(BMI)
c) Nối A với I:
Ta có: S(AMI) = 1/2 S(BMI) (Vì đáy AM = 1/2 đáy BM ; chung chiều cao hạ từ I xuống AB)
S(ANI) = 1/2 S(CNI)
Mà S(CNI) = S(BMI) nên S(AMI) = S(ANI) = 90 : 2 = 45 cm2
=> S(AIB) = 3 x S(AMI) = 3 x 45 = 135 cm2
=>S(ABN) = S(AIB) + S(AIN) = 135 + 45 = 180 cm2
=> S(ABC) = 3 x S(ABN) = 3 x 180 = 540 cm2
Theo bài ra ta có: BE = 1/2 EC. Suy ra: BE = 1/3 BC
Suy ra:
SABE = 1/3 SABC
SAEC = 2/3 SABC
Theo bài ra ta cũng có: EC = 2/3 BC
Suy ra: SABI = 2/3 SABE
Suy ra:
SABI = (2/3 x 1/3) SABC = 2/9 SABC
SBIE = 1/2 SABI = 1/9 SABC
Ta lại có: SCIE = 2 SBIE
Suy ra: SCIE = 2/9 SABC
Ta có: SBIC = SBIE + SCIE = 1/9 SABC + 2/9 SABC = 3/9 SABC
Hai tam giác ABI và BIC có BI chung nên 2 đường cao tỉ lệ với 2 diện tích và bằng: (2/9) : (3/9) = 2/3. Do 2 đường cao này cũng là 2 đường cao của 2 tam giác AID và CID có chung ID nên ta có: SAID : SCID = 2/3
Suy ra: SCID = 16 : 2/3 = 24 (cm2)
Suy ra: SAIC = SAID + SCID = 16 + 24 = 40 (cm2)
Vì: SAIC = 2/3 SAEC, suy ra: SAEC = 3/2 SAIC = 3/2 x 40 = 60 (cm2)
Vì: SAEC = 2/3 SABC, suy ra: SABC = 3/2 SAIC = 3/2 x 60 = 90 (cm2)
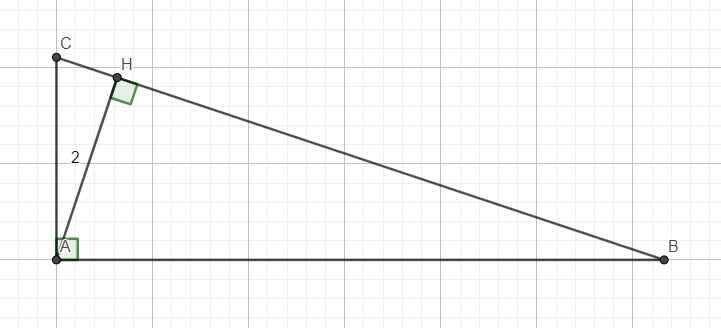
Cho tam giác ABC vuông tại A, AH vuông góc với BC,có AH=2, tan B=1/3. Tính AB, AC. Mong mn giúp mình
Trong tam giác vuông ABH ta có:
\(tanB=\dfrac{AH}{BH}\Rightarrow BH=\dfrac{AH}{tanB}=6\)
Áp dụng định lý Pitago:
\(AB^2=AH^2+BH^2=40\)
\(\Rightarrow AB=2\sqrt{10}\)
Trong tam giác vuông ABC:
\(tanB=\dfrac{AC}{AB}\Rightarrow AC=AB.tanB=\dfrac{2\sqrt{10}}{3}\)
-Tham khảo:
https://olm.vn/hoi-dap/tim-kiem?q=cho+tam+gi%C3%A1c+ABC.+G%C3%B3c+A+=+30+%C4%91%E1%BB%99+.+D%E1%BB%B1ng+%E1%BB%9F+ngo%C3%A0i+tam+gi%C3%A1c+ABC+tam+gi%C3%A1c+%C4%91%E1%BB%81u+BCD.+CMR:+AD%5E2=AB%5E2+AC%5E2&id=818425
Đáp án C