Chứng minh rằng các hàm số F(x) và G(x) sau đều là một nguyên hàm của cùng một hàm số:
K
Khách
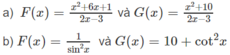
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
12 tháng 6 2018
- Vì F(x) và G(x) đều là nguyên hàm của f(x) nên tồn tại một hằng số C sao cho: F(x) = G(x) + C
- Khi đó F(b) – F(a) = G(b) + C – G(a) – C = G(b) – G(a).
a) Vì
nên F(x) và G(x) đều là một nguyên hàm của
b) Vì
nên F(x) và G(x) đều là một nguyên hàm của