Tìm điều kiện của các phương trình sau x x - 1 = 2 x + 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta thấy x + 2 ≠ 0 khi x ≠ - 2 và x - 2 ≠ 0 khi x ≠ 2.
Do đó ĐKXĐ của phương trình (x - 1)/(x + 2) + 1 = 1/(x - 2) là x ≠ ± 2.

1B
2D
3A
4A
5B
6:
a: \(A=\dfrac{14+2}{3}=\dfrac{16}{3}\)
b: P=A*B
\(=\dfrac{x+2}{3}\cdot\dfrac{2x^2+6x-2x^2-3x-9}{\left(x-3\right)\left(x+3\right)}\)
\(=\dfrac{x+2}{3}\cdot\dfrac{3x-9}{\left(x-3\right)\left(x+3\right)}=\dfrac{x+2}{x+3}\)

x ≥ 2 và x ≤ -4. Không có số thực x nào thỏa mãn điều kiện của phương trình.

a)\(x\in R\)
b)\(x\ne1\)
c) \(x\notin\left\{1;2\right\}\)
d) \(x\notin\left\{3;-3\right\}\)
e) \(x\ne1\)
f) \(x\notin\left\{2;3\right\}\)

Điều kiện của phương trình là x ≥ 1; x ≠ 2 và x ≠ -2. Vì x > -1 thì x ≠ 2. Vì x > -1 thì x ≠ -2 suy ra điều kiện của phương trình là x ≥ -1; x ≠ 2

a: Để đây là phương trình bậc nhất một ẩn thì m+3<>0
hay m<>-3
b: Để đây là phươg trình bậc nhất một ẩn thì m<>0

Ta thấy 1 - 2x ≠ 0 khi x ≠ 1/2.
Do đó ĐKXĐ của phương trình (x - 1)/(1 - 2x) = 1 là x ≠ 1/2.

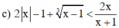
BPT xác định khi x + 1 ≠ 0 ⇔ x ≠ –1.
Vậy tập giá trị của x thỏa mãn điều kiện xác định là D = R\{–1}

ĐKXĐ: `{(5x-1>=0),(x+2>=0),(7-x>=0):}`
`<=>{(x>=1/5),(x>=-2),(x<=7):}`
`<=>1/5 <=x<=7`
`ĐKXĐ: {(5x - 1 >= 0),(x+2 >=0),(7-x >=0):}`
`<=> {(x >= 1/5),(x>= -2),(x <=7):}`
`<=> 1/5 <= x <= 7`
Biểu thức vế trái có nghĩa khi x > 1 và biểu thức vế phải có nghĩa khi . Từ đó suy ra điều kiện của phương trình là x > 1.