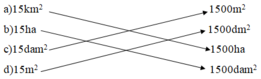
Nối hai số đo diện tích bằng nhau
a ) 15 k m 2 1500 m 2 b ) 15 h a 1500 d m 2 c ) 15 d a m 2 1500 h a d ) 15 m 2 1500 d a m 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có:
*S ABCD = S ABC + S ACD
Hay
S ABCD = S 1 + S 2 + S 3 + S 4 + S 5 + S 6 + S 7 + S 8
*Vì MB = MC nên:
S1 + S2 = S ABC : 2 ( Tam giác ABM và ABC có chung đường cao hạ từ A và BM = BC : 2 )
*Tương tự: S 7 + S 8 = S ACD : 2 ( Tam giác CED và ACD có chung đường cao hạ từ C và DE = AD : 2 )
*Do đó:
S 1 + S 2 + S 7 + S 8 = S 3 + S 4 + S 5 + S 6 = S ABCD : 2
*Lại có:
S 2 + S 3 = S 5 + S 6 (Hai tam giác BME và CME có chung đường cao hạ từ E và BM = CM)
S 5 + S 8 = S 3 + S 4 (Hai tam giác AME và DME có chung đường cao hạ từ M và ED = EA)
==>S 2 + S 8 = S 4 + S 6
*Vì S 1 + S 7 + (S 2 + S 8) = S 3 + S 5 + (S 4 + S 6) mà S 2 + S 8 = S 4 + S 6
Nên S 1 + S 7 = S 3 + S 5
==>S 3 + S 5 = 3 cm2 + 5 cm2 = 8 cm2
Hay SEHKMN = 8 cm2
Đáp số : 8 cm2

AN = 2/3 AI ==> NI = 1/3 AI
SAIM = SMNI x 3 (AI=NI x 3, chung đường cao kẻ từ M).
SAIM = 15 x 3 = 45 (cm2)
SABM = SAIM x 2 (BM=IM x 2, chung đường cao kẻ từ A).
SABM = 45 x 2 = 90 (cm2)
Xét 3 tam giác ABM ; BMC và AMD. Ta thấy AB = MD+MC (chiều dài hình chữ nhật), 3 tam giác này có 3 đường cao bằng nhau bằng chiều rộng hình chữ nhật nên.
SABM = SBMC + SAMD = 90 cm2.
Diện tích hình chữ nhật ABCD
90 x 2 = 180 (cm2)
ai k mk mk k lại

diện tích hình tam giác CMD là:
15 ÷ 4 × 7 = 26,25 (cm2)
diện tích hình tam giác BCD là:
15 + 26,25 = 41,25 (cm2)
Diện tích tam giác ABC là:
41,25 ÷ 7 × 4 = 1657 ( cm2)
Diện tích hình thang ABCD là:
23,57 + 41,25 = 64,82 ( cm2)
Đ/s : 64,82 cm2

Xét tam giác \(ABC\) và tam giác \(ACD\) có \(\frac{AD}{CD}=\frac{4}{7}\) khoảng cách từ \(A\) xuống \(DC\) bằng khoảng cách từ \(C\) xuống \(AB\) nên \(\frac{S_{ABC}}{S_{ACD}}=\frac{4}{7}\)
Xét tam giác \(ABC\) và tam giác \(ACD\) có chung đáy \(AC\)\(\frac{S_{ABC}}{S_{ACD}}=\frac{4}{7}\) nên khoảng cách từ \(B\) đến \(AC\) bằng \(\frac{4}{7}\) khoảng cách từ \(D\) đến \(AC\)
Xét tam giác \(BMC\) và tam giác \(DMC\) có chung đáy \(MC\) khoảng cách từ \(B\)đến \(AC\) bằng\(\frac{4}{7}\) khoảng cách từ \(D\) đến \(AC\) nên \(\frac{S_{BMC}}{S_{CMD}}=\frac{4}{7}\)
Diện tích tam giác \(CMD\) là:
\(15\div4\times7=26,25\)( cm2 )
Diện tích tam giác \(BCD\) là:
\(15+26,25=41,25\)( cm2 )
Diện tích tam giác \(ABC\) là:
\(41,25\div7\times4=\frac{165}{7}=23,57\)( cm2 )
Diện tích hình thang \(ABCD\) là:
\(23,57+41,25=64,82\)( cm2 )
Đáp số : \(64,82\)cm2

bài này ko giống của lớp 5 ??? mà Nobita Kun mới hok cx có thể xem lại cách làm được mà!!!
4577