Số nghiệm trong khoảng có phương trình sin2x = cos2x là:
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án A
sin 2 x = c os2x ⇔ 2 sin ( 2 x − π 4 ) = 0 ⇔ 2 x = π 4 + k π ⇔ x = π 8 + k π 2

Đáp án: C
Vì f'(x) = ( x 5 + x 3 - 7)' = 5 x 4 + 3 x 2 ≥ 0, ∀x ∈ R (dấu "=" xảy ra ⇔ x = 0). Suy ra f(x) đồng biến trên R. Mặt khác f(0) = -7, f(2) = 32 + 8 - 7 = 33 > 0. Hàm f(x) liên tục trên đoạn [0;2] nên tồn tại x0 ∈ (0;2) để f(x0) = 0. Suy ra f(x) = 0 có nghiệm duy nhất trên R.
Cách khác: Phương trình 3 sin 2 x - cos 2 x + 5 = 0
⇔ 3 sin 2 x + sin 2 x + 4 = 4( sin 2 x + 1) = 0, vô nghiệm
Các phương trình x 2 - 5x + 6 = 0 và 3tanx - 4 = 0 có nhiều hơn một nghiệm. Từ đó suy ra phương trình x 5 + x 3 - 7 = 0 có nghiệm duy nhất trên R.

Đáp án: C
Vì f'(x) = ( x 5 + x 3 - 7)' = 5 x 4 + 3 x 2 ≥ 0, ∀ x ∈ R (dấu "=" xảy ra ⇔ x = 0). Suy ra f(x) đồng biến trên R. Mặt khác f(0) = -7, f(2) = 32 + 8 - 7 = 33 > 0. Hàm f(x) liên tục trên đoạn [0;2] nên tồn tại x 0 ∈ (0;2) để f( x 0 ) = 0. Suy ra f(x) = 0 có nghiệm duy nhất trên R.
Cách khác: Phương trình 3 sin 2 x + c o s 2 x + 5 = 0
⇔ 3 sin 2 x + sin 2 x + 4 = 4( sin 2 x + 1) = 0, vô nghiệm
Các phương trình x 2 - 5x + 6 = 0 và 3tanx - 4 = 0 có nhiều hơn một nghiệm. Từ đó suy ra phương trình x 5 + x 3 - 7 = 0 có nghiệm duy nhất trên R.

Phương trình ⇔ cos 2 x − sin 2 x − sin 2 x = 2 ⇔ cos 2 x − sin 2 x = 2
⇔ cos 2 x + π 4 = 1 ⇔ 2 x + π 4 = k 2 π ⇔ x = − π 8 + k π k ∈ ℤ . 0 < x < 2 π ⇒ 0 < − π 8 + k π < 2 π ⇔ 1 8 < k < 17 8 → k ∈ ℤ k = 1 → x = 7 π 8 k = 2 → x = 15 π 8 ⇒ T = 7 π 8 + 15 π 8 = 11 4 π .
Chọn đáp án C.

Pt \(\Leftrightarrow2sin\left(2x+\dfrac{\pi}{3}\right)=\sqrt{3}\)
\(\Leftrightarrow sin\left(2x+\dfrac{\pi}{3}\right)=\dfrac{\sqrt{3}}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k\pi\\x=k\pi\end{matrix}\right.\)\(\left(k\in Z\right)\)
\(x\in\left(0;\dfrac{\pi}{2}\right)\)\(\Rightarrow\left[{}\begin{matrix}0< \dfrac{\pi}{6}+k\pi< \dfrac{\pi}{2}\\0< k\pi< \dfrac{\pi}{2}\end{matrix}\right.\)\(\left(k\in Z\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}-\dfrac{1}{6}< k< \dfrac{1}{3}\\0< k< \dfrac{1}{2}\end{matrix}\right.\)\(\left(k\in Z\right)\)\(\Leftrightarrow\left[{}\begin{matrix}k=0\\k\in\varnothing\end{matrix}\right.\)
Vậy có 1 nghiệm thỏa mãn
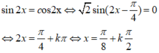
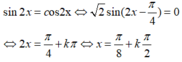
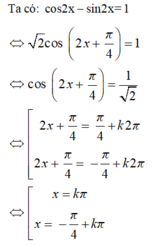

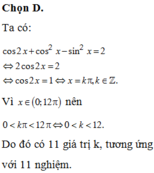
Đáp án A