Trong mặt phẳng Oxy, cho hình chữ nhật OMNP với và Gọi S là tập hợp tất cả các điểm với nằm bên trong (kể cả trên cạnh) của OMNP . Lấy ngẫu nhiên một điểm Xác suất để bằng:
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Số phần tử của không gian mẫu tập hợp các điểm có tọa độ nguyên nằm trên hình chữ nhật OMNP là
n Ω = 101 x 11
![]()
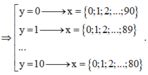
Khi đó có 91 + 90 + . . . + 81 = 946 cặp (x;y) thỏa mãn
Vậy xác suất cần tính là
![]()

Chọn đáp án D.
Số phần tử của không gian mẫu tập hợp các điểm có tọa độ nguyên nằm trên hình chữ nhật OMNP là n(Ω)=101x11
Vì x ϵ [0;100];y ϵ [0;10] và x+y ≤90 ⇒ y = 0 → x = 0 ; 1 ; 2 ; . . . ; 90 y = 1 → x = 0 ; 1 ; 2 ; . . . ; 89 . . . y = 10 → x = 0 ; 1 ; 2 ; . . . ; 80
Khi đó có 91 + 90 + … + 81 = 946 cặp (x;y) thỏa mãn.
Vậy xác suất cần tính là P=n(X)/n(Ω)=86/101

Điểm A(x;y) nằm bên trong (kể cả trên cạnh) của
![]()
Có 101 cách chọn x, 11 cách chọn y. Do đó số phần tử của không gian mẫu tập hợp các điểm có tọa độ nguyên nằm trên hình chữ nhật OMNP là n( Ω ) = 101 x 11
Gọi X là biến cố: “Các điểm A(x;y) thỏa mãn x + y ≤ 90”.
Vì
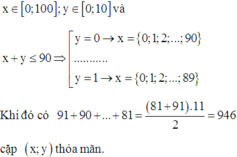
Vậy xác suất cần tính là

I là trung điểm AC \(\Rightarrow C\left(2;-2\right)\)
\(\Rightarrow\overrightarrow{CM}=\left(2;-1\right)\Rightarrow\) đường thẳng BC có dạng:
\(1\left(x-2\right)+2\left(y+2\right)=0\Leftrightarrow x+2y+2=0\)
Đường thẳng AB qua A và vuông góc BC nên nhận \(\left(2;-1\right)\) là 1 vtpt
Phương trình AB:
\(2\left(x+1\right)-1\left(y-2\right)=0\Leftrightarrow2x-y+4=0\)
B là giao điểm AB và BC nên tọa độ là nghiệm:
\(\left\{{}\begin{matrix}x+2y+2=0\\2x-y+4=0\end{matrix}\right.\) \(\Rightarrow B\left(...\right)\)
I là trung điểm BD \(\Rightarrow\left\{{}\begin{matrix}x_D=2x_I-x_B=...\\y_D=2y_I-y_B=...\end{matrix}\right.\)

AB đi qua E và vuông góc BC nên nhận (1;-1) là 1 vtpt
Phương trình AB:
\(1\left(x+1\right)-1\left(y-1\right)=0\Leftrightarrow x-y+2=0\)
Tọa độ B là nghiệm: \(\left\{{}\begin{matrix}x-y+2=0\\x+y+4=0\end{matrix}\right.\) \(\Rightarrow B\left(-3;-1\right)\)
Đường thẳng d qua M và song song AB có pt:
\(1\left(x+1\right)-1\left(y+1\right)=0\Leftrightarrow x-y=0\)
Gọi N là giao điểm d và BC \(\Rightarrow N\) là trung điểm BC
Tọa độ N là nghiệm: \(\left\{{}\begin{matrix}x-y=0\\x+y-4=0\end{matrix}\right.\) \(\Rightarrow N\left(2;2\right)\Rightarrow C\left(7;5\right)\)
Đường thẳng AD qua M và song song BC có pt:
\(1\left(x+1\right)+1\left(y+1\right)=0\Leftrightarrow x+y+2=0\)
A là giao điểm AB và AD nên tọa độ là nghiệm: \(\left\{{}\begin{matrix}x-y+2=0\\x+y+2=0\end{matrix}\right.\) \(\Rightarrow A\left(-2;0\right)\)
\(\overrightarrow{AB}=\overrightarrow{DC}\Rightarrow\) tọa độ D

Phương trình đường thẳng qua O và song song AB có dạng: x−y=0x−y=0
⇒⇒ Tọa độ M là nghiệm của hệ: {x+3y−6=0x−y=0{x+3y−6=0x−y=0 ⇒M(32;32)⇒M(32;32)
Phương trình đường thẳng BC qua M, nhận (1;1)(1;1) là 1 vtpt có dạng:
1(x−32)+1(y−32)=0⇔x+y−3=01(x−32)+1(y−32)=0⇔x+y−3=0
Tọa độ B là nghiệm của hệ: {x−y+5=0x




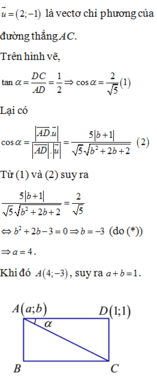
Đáp án D.
Số phần tử của không gian mẫu tập hợp các điểm có tọa độ nguyên nằm trên hình chữ nhật OMNP là n Ω = 101 × 11.
Vì x ∈ 0 ; 100 ; y ∈ 0 ; 10 và x + y ≤ 90
⇒ y = 0 → x = 0 ; 1 ; 2 ; ... ; 90 y = 1 → x = 0 ; 1 ; 2 ; ... ; 89 ... y = 10 → x = 0 ; 1 ; 2 ; ... ; 80 .
Khi đó có 91 + 90 + ... + 81 = 946 cặp x ; y thỏa mãn.
Vậy xác suất cần tính là:
P = n ( X ) n Ω = 946 101 × 11 = 86 101 .