Tìm 2 số tự nhiên biết tổng của chúng bằng 84, ƯCLN của chúng bằng 6
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


- Gọi 2 số phải tìm là `a` và `b` `(a,b in ZZ)`
- Giả sử `a>=b`
- Vì UCLN(a,b)=6
$\Rightarrow \begin{cases} a=6m\\b=6n\end{cases}$
`(m,n in ZZ; UCLN(m,n)=1,m>=n)`
- Theo đề bài ta có : `a+b=84`
`=> 6m+6n=84`
`=> 6(m+n)=84`
`=> m+n=14`
- Chọn m và n nguyên tố cùng nhau, `m>=n` và `m+n=14` ta được các cặp số `(m,n)` là : `(13,1);(11,3);(9,5)`
+ Với `(m,n)=(13,1)` thì :
$\begin{cases} a=6.13=78\\b=6.1=6\end{cases}$
+ Với `(m,n)=(11,3)` thì :
$\begin{cases} a=6.11=66\\b=6.3=18\end{cases}$
+ Với `(m,n)=(9,5)` thì :
$\begin{cases} a=6.9=54\\b=6.5=30\end{cases}$
- Vậy ta tìm được các cặp số thỏa mãn :
+ 78 và 6
+ 66 và 18
+ 54 và 30

a, Gọi hai số tự nhiên cần tìm là a và b
Ta có : \(a=6.k_1;b=6.k_2\)
Trong đó : \(ƯCLN\left(k_1,k_2\right)=1\)
Mà : \(a+b=84\Rightarrow6.k_1+6.k_2=84\)
\(\Rightarrow6\left(k_1+k_2\right)=84\Rightarrow k_1+k_2=84\div6=14\)
+) Nếu : \(k_1=1\Rightarrow k_2=13\Rightarrow\begin{cases}a=6\\b=78\end{cases}\)
+)Nếu : \(k_1=3\Rightarrow k_2=11\Rightarrow\begin{cases}a=18\\b=66\end{cases}\)
+)Nếu : \(k_1=5\Rightarrow k_2=9\Rightarrow\begin{cases}a=30\\b=54\end{cases}\)
Vậy ...
b, Tương tự câu a,
c, Gọi hai số tự nhiên cần tìm là a và b
Vì : \(ƯCLN\left(a,b\right)=10;BCNN\left(a,b\right)=900\)
\(\RightarrowƯCLN\left(a,b\right).BCNN\left(a,b\right)=a.b=900.10=9000\)
Phần còn lại giống câu a và câu b tự làm

Gọi hai số phải tìm là a và b ( a < b ). Ta có ( a,b ) = 6 nên a = 6a', b = 6b' trong đó ( a' b' ) = 1 ( a,b, a', b' \(\in\) N ).
Do a + b = 84 nên 6(a' + b' ) = 84 suy ra a' + b' = 14.
Chọn cặp số a' , b' nguyên tố cùng nhau có tổng bằng 14 ( a' < b' ), ta được
| a' | 1 | 3 | 5 |
| b' | 13 | 11 | 9 |
Do đó
| a | 6 | 18 | 30 |
| b | 78 | 66 | 54 |
a+b=84 (a<b; a,b thuộc N*)
UCLN(a,b)=6 => {a=6m {b=6m
(m,n)=1 và m,n thuộc N*
a+b=84 => 6m+6n=84 => m+n=14
*m=1=> n=13 => a=6, b=78
*m=3=> n=11 => a=18, b=66
*m=5 => n=9 => a= 30, b=54
Vậy (a,b) = (6,78); (18,66); (30,54)

Gọi 2 số tự nhiên đó là a và b.
Do ƯCLN(a;b) = 12 => a = 12m ; b = 12n (với m,n là 2 số nguyên tố cùng nhau)
Ta có : a - b = 12(m - n) = 84
=> m - n = 7
Mà m,n nguyên tố cùng nhau và ƯCLN(12m; 12n) = 1 => m = 8 ; n = 1
=> a = 96 ; b = 12
Vậy 2 số cần tìm là 96 và 12

Gọi hai số cần tìm là a và b. Giả sử a ≤ b. Ta có :
ƯCLN(a ; b) = 6 ⇒ a = 6m và b = 6n (m,n ∈ N* và m ≥ n ; m,n nguyên tố cùng nhau)
Do đó a + b = 6m + 6n = 6.(m + n) = 84
⇒ m + n = 14. Vì m ≥ n và m,n ∈ N* và m,n nguyên tố cùng nhau nên ta có bảng sau :
m | 13 |
| 11 |
| 9 |
|
|
a | 78 |
| 66 |
| 54 |
|
|
n | 1 |
| 3 |
| 5 |
|
|
b | 6 |
| 18 |
| 30 |
|
|
Vậy (a;b) ∈ {(78;6);(66;18);(54;30)}
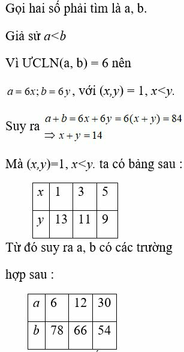
Gọi hai số phải tìm là a, b.
Giả sử a<b
Vì ƯCLN(a,b)=6 nên a = 6x ; b = 6y với (x,y)=1, x < y.
Suy ra a+b = 6x+6y = 6(x+y) = 84 => x+y = 14
Mà (x,y)=1, x < y. ta có bảng sau :
Từ đó suy ra a, b có các trường hợp sau :