Cho tam giác ABC và điểm M thỏa mãn Khi đó điểm M là:
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1.
Lấy điểm A' đối xứng với A qua Ox \(\Rightarrow A\left(-2;-1\right)\)
M có tọa độ \(M\left(x;0\right)\)
Ta có \(AM+MB=A'M+MB\ge AB=\sqrt{4^2+5^2}=\sqrt{41}\)
\(min=41\Leftrightarrow M,A',B\) thẳng hàng
\(\Leftrightarrow\overrightarrow{A'M}=k\overrightarrow{A'B}\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+2=k.4\\1=k.5\end{matrix}\right.\Rightarrow x=-\dfrac{6}{5}\Rightarrow M\left(-\dfrac{6}{5};0\right)\)
2.
Gọi N là trung điểm BC
\(\overrightarrow{MA}.\left(\overrightarrow{MB}+\overrightarrow{MC}\right)=0\)
\(\Leftrightarrow2\overrightarrow{MA}.\overrightarrow{MN}=0\)
\(\Leftrightarrow2MA.MN.cosAMN=0\)
\(\Leftrightarrow\left[{}\begin{matrix}MA=0\\MN=0\\cosAMN=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}M\equiv A\\M\equiv N\\\widehat{AMN}=90^o\end{matrix}\right.\)
\(\Rightarrow M\) thuộc đường tròn đường kính AN
cho tam giác abc và 2 điểm M,N thỏa mãn điều kiện MA+3MC=0,NA+2NB+3NC=0,chưmgs minh b,m,n thẳng hàng

vecto NA+2*vecto NB+3*vecto NC=vecto 0
=>2*vecto NB=-vecto NA-3 vecto NC
=>vecto NB=-1/2*vecto NA-3/2*vecto NC
=-1/2(vecto NM+vecto MA)-3/2(vecto NM+vecto MC)
=-2vecto NM-1/2vecto MA-3/2vecto MC
=-2 vecto NM-1/2(vecto MA+3 vecto MC)
=-2 vecto NM
=>vecto BN=2*vecto MN
=>B,M,N thẳng hàng
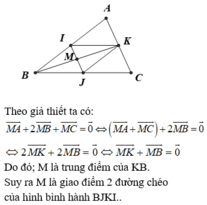

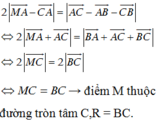
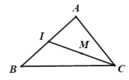

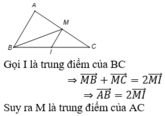
Đáp án C