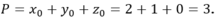Trong không gian với hệ tọa độ Oxyz, cho ba điểm A (2; -3; 7), B (0; 4; -3) và C (4; 2; 5). Biết điểm nằm trên (Oxy) sao cho có giá trị nhỏ nhất. Khi đó tổng bằng:
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A.
M là điểm thuộc tia đối của tia BA sao cho A M B M = 2 nên B là trung điểm của AM.


Chọn C.
Phương pháp: Hai véc tơ bằng nhau khi và chỉ khi các tọa độ tương ứng bằng nhau.


Đáp án là D.
+ Gọi H x ; y ; z là chân đường phân giác trong góc A của Δ A B C .
Ta có: H B → H C → = − A B A C = − 2
⇔ H B → = − 2 H C → ⇒ H − 5 3 ; 8 3 ; 0 ⇒ A H = 2 74 3 .


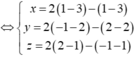
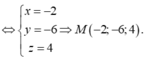

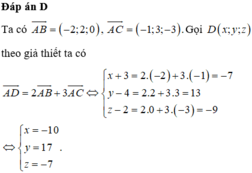


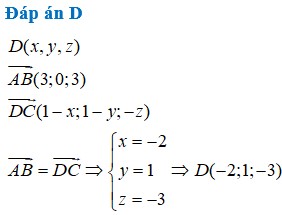
Chọn C
Gọi G là trọng tâm tam giác ABC => G = (2; 1; 3)
Khi đó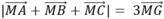
Nên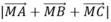 có giá trị nhỏ nhất khi và chỉ khi MG ngắn nhất, khi đó M là hình chiếu vuông góc của G (2; 1; 3) trên (Oxy)
có giá trị nhỏ nhất khi và chỉ khi MG ngắn nhất, khi đó M là hình chiếu vuông góc của G (2; 1; 3) trên (Oxy)
Do đó M (2; 1; 0).
Vậy