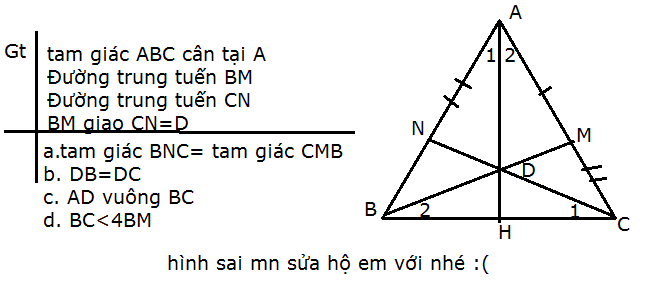
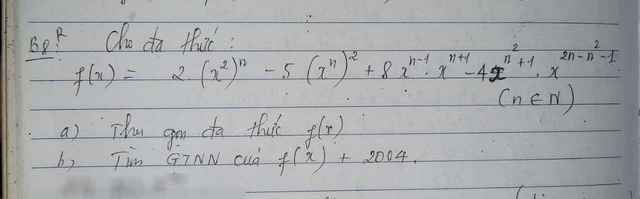Làm phần a,b thôi cũng đc ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NP
0
Những câu hỏi liên quan
MT
2
24 tháng 10 2021
\(P=A.B=\dfrac{\sqrt{x}-1}{\sqrt{x}-3}.\dfrac{\sqrt{x}+6}{\sqrt{x}-1}=\dfrac{\sqrt{x}+6}{\sqrt{x}-3}\)
\(=1+\dfrac{9}{\sqrt{x}-3}\le1+\dfrac{9}{0-3}=1-3=-2\)
\(maxP=-2\Leftrightarrow x=0\)
24 tháng 10 2021
\(1,x=16\Leftrightarrow A=\dfrac{4-1}{4-3}=\dfrac{3}{1}=3\\ 2,B=\dfrac{x+2\sqrt{x}-3+5\sqrt{x}+5+4}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{x+7\sqrt{x}+6}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ B=\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}+6\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{\sqrt{x}+6}{\sqrt{x}-1}\\ 3,P=AB=\dfrac{\sqrt{x}-1}{\sqrt{x}-3}\cdot\dfrac{\sqrt{x}+6}{\sqrt{x}-1}=\dfrac{\sqrt{x}+6}{\sqrt{x}-3}\\ P=1+\dfrac{9}{\sqrt{x}-3}\\ Vì.\sqrt{x}-3\ge-3\Leftrightarrow\dfrac{9}{\sqrt{x}-3}\le-3\\ \Leftrightarrow P=1+\dfrac{9}{\sqrt{x}-3}\le1-3=-2\\ P_{max}=-2\Leftrightarrow x=0\)
22 tháng 3 2023
BT4: Hiệu suất phản ứng:
\(H=\dfrac{m_{tt}}{m_{lt}}.100\%=\dfrac{36,48}{48}.100\%=76\%\)
BT5 Khối lượng đồng thu được:
\(H=\dfrac{m_{tt}}{m_{lt}}.100\%\Rightarrow m_{tt}=\dfrac{m_{lt}.H}{100\%}=\dfrac{48.95}{100\%}=45,6\left(g\right)\)
K
13 tháng 12 2020
11 c)
\(a^2+2\ge2\sqrt{a^2+1}\Leftrightarrow a^2+1-2\sqrt{a^2+1}+1\ge0\Leftrightarrow\left(\sqrt{a^2+1}-1\right)^2\ge0\) (luôn đúng)
K
13 tháng 12 2020
12 a) Có a+b+c=1\(\Rightarrow\) (1-a)(1-b)(1-c)= (b+c)(a+c)(a+b) (*)
áp dụng BĐT cô-si: \(\left(b+c\right)\left(a+c\right)\left(a+b\right)\ge2\sqrt{bc}2\sqrt{ac}2\sqrt{ab}=8\sqrt{\left(abc\right)2}=8abc\) ( luôn đúng với mọi a,b,c ko âm )
b) áp dụng BĐT cô-si: \(c\left(a+b\right)\le\dfrac{\left(a+b+c\right)^2}{4}=\dfrac{1}{4}\)
Tương tự: \(a\left(b+c\right)\le\dfrac{1}{4};b\left(c+a\right)\le\dfrac{1}{4}\)
\(\Rightarrow abc\left(a+b\right)\left(b+c\right)\left(c+a\right)\le\dfrac{1}{4}\dfrac{1}{4}\dfrac{1}{4}=\dfrac{1}{64}\)
28 tháng 5 2021
a) Có \(\widehat{OAM}=90^0\) => Tam giác \(OAM\) nội tiếp đường tròn đường kính OM
=> O,A,M cùng thuộc đường tròn đường kính OM (*)
Có \(\widehat{OBM}=90^0\) => Tam giác \(OBM\) nội tiếp đường tròn đường kính OM
=> O,B,M cùng thuộc đường tròn đường kính OM (2*)
Do N là trung điểm của PQ => \(ON\perp PQ\)( Vì trong một đt, đường kính đi qua trung điểm của một dây ko đi qua tâm thì vuông góc với dây ấy)
=> \(\widehat{ONM}=90^0\) => Tam giác \(ONM\) nội tiếp đường tròn đường kính OM
=> O,N,M cùng thuộc đt đường kính OM (3*)
Từ (*) (2*) (3*) => O,M,N,A,B cùng thuộc đt đk OM hay đt bán kính \(\dfrac{OM}{2}\)
b) Có AM//PS (cùng vuông góc với OA)
Gọi E là gđ của PS với (O) => \(sđ\stackrel\frown{AE}=sđ\stackrel\frown{AP}\)
Có \(\widehat{PRB}=\dfrac{1}{2}\left(sđ\stackrel\frown{AE}+sđ\stackrel\frown{PB}\right)\)\(=\dfrac{1}{2}\left(sđ\stackrel\frown{AP}+sđ\stackrel\frown{PB}\right)=\dfrac{1}{2}sđ\stackrel\frown{AB}\)
=> \(\widehat{PRB}=\widehat{MAB}=\dfrac{1}{2}sđ\stackrel\frown{AB}\)
Có BNAM nội tiếp => \(\widehat{MAB}=\widehat{MNB}\)
\(\Rightarrow\widehat{PRB}=\widehat{MNP}\) => PRNB nội tiếp
\(\Rightarrow\widehat{BRN}=\widehat{BPN}\) mà \(\widehat{BPN}=\widehat{BAQ}=\dfrac{1}{2}sđ\stackrel\frown{BQ}\)
\(\Rightarrow\widehat{BRN}=\widehat{BAQ}\) => RN//AQ hay RN // SQ mà N la trung điểm của PQ
=> RN là đường TB của tam giác PSQ
=> R là trung điểm của PS <=> PR=RS
NT
1
13 tháng 11 2023
Câu 2:
a:
\(10=2\cdot5;12=2^2\cdot3;18=3^2\cdot2\)
=>\(BCNN\left(10;12;18\right)=3^2\cdot2^2\cdot5=180\)
\(x⋮10;x⋮12;x⋮18\)
=>\(x\in BC\left(10;12;18\right)\)
=>\(x\in B\left(180\right)\)
=>\(x\in\left\{180;360;540;...\right\}\)
mà 100<x<500
nên \(x\in\left\{180;360\right\}\)
b:
\(72=2^3\cdot3^2;24=2^3\cdot3;120=2^3\cdot3\cdot5\)
=>\(ƯCLN\left(72;24;120\right)=2^3\cdot3=24\)
\(72⋮x;24⋮x;120⋮x\)
=>\(x\inƯC\left(72;24;120\right)\)
=>\(x\inƯ\left(24\right)\)
=>\(x\in\left\{1;2;3;4;6;8;12;24\right\}\)
mà 5<x<10
nên \(x\in\left\{6;8\right\}\)
28 tháng 11 2021
Nếu đề bài yêu cầu tính A, B thì chỉ cần thay giá trị của x vào rồi tính như bth là được nhé
