Hệ bất phương trình có tập nghiệm là khoảng khi và chỉ khi
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

hoc gioi the hihiihihihhhihihihihiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiii
,mnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnn

bpt (1) \(\Leftrightarrow x\in\left(-5;3\right)\)=> S1=(-5;3)
bpt (2):
Nếu m=-1 =>S2=\(\varnothing\)
Nếu m>-1 =>S2=\(\left[\frac{3}{m+1};+\infty\right]\)
Nếu m<-1 => S2=\(\left[-\infty;\frac{3}{m+1}\right]\)
Hệ có nghiệm \(\Leftrightarrow S1\cap S2\ne\varnothing\)
Nếu m=-1 =>\(S1\cap S2=\varnothing\) (Loại)
Nếu m>-1 =>\(S1\cap S2\ne\varnothing\)
Nếu m<-1 =>\(S1\cap S2\ne\varnothing\)
vì sao mà hệ có nghiệm thì S1 giao S2 phải khác tập hợp rỗng ? mà tại sao bạn lại biện luận bất phương trình như vậy ?

bpt (1) : x> \(\frac{2m}{3m-1}\); bpt (2) : x > \(\frac{m}{2}\)
de 2 bpt co cung tap nghiem thi \(\frac{2m}{3m-1}\)= \(\frac{m}{2}\)(3) voi dk m # \(\frac{1}{3}\)
giai pt (3) tim duoc m= 0 , m = \(\frac{5}{3}\)thoa dieu kien m # \(\frac{1}{3}\)

Chọn B.
Ta có:
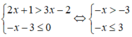
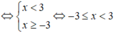
Tập nghiệm của hệ bất phương trình là S = [-3;3).
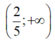
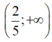
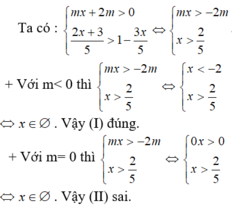
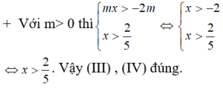
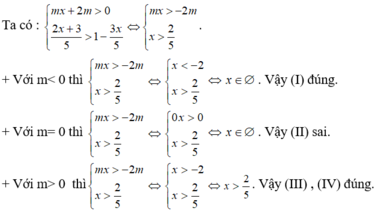
Ta có: 2 x - 1 > 0 ⇔ 2 x > 1 ⇔ x > 1 2
* Xét bất phương trình mx – 3 < 0 (*)
+ Nếu m = 0 thì (*) luôn đúng với mọi x. khi đó, nghiệm của hệ bất phương trình là: 1 2 ; + ∞
+ Nếu m < 0 thì (*): m x < 3 ⇔ x > 3 m
Khi đó, tập nghiệm của hệ bất phương trình là: m a x 1 2 ; 3 m ; + ∞
+ Nếu m >0 thì (*) m x < 3 ⇔ x < 3 m
Để hệ bất phương trình có tập nghiệm là khoảng 1 2 ; 2 thì 3 m = 2 ⇔ m = 3 2
Kết luận: Để hệ bất phương trình có tập nghiệm là khoảng 1 2 ; 2 thì m = 3 2