Cho tam giác ABC và đường trung tuyến AM. Chứng minh SAMB = SAMC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
QT
1
DT
16 tháng 12 2021
vẽ đường cao AH chung của tam giác AMB và AMC
SAMB=\(\dfrac{1}{2}\)BM.AH
SAMC=\(\dfrac{1}{2}\)CM.AH
Vì AM là đường trung tuyến nên BM=MC
Do đó:SAMC=SAMB
( cái đường cao AH vuông góc với BC ă)
S
subjects
CTVHS
4 tháng 3 2023
câu 2 :
a) có phải là chứng minh AM ⊥ BC không
xét ΔAMB và ΔAMC, ta có :
AB = AC (2 cạnh bên của ΔABC cân tại A)
MB = MC (AM là đường trung tuyến của cạnh BC)
AM là cạnh chung
=> ΔAMB = ΔAMC (c.c.c)
=> \(\widehat{AMB}=\widehat{AMC}\) (2 cạnh tương ứng)
mà \(\widehat{AMB}+\widehat{AMC}=180^O\) (kề bù)
\(\Rightarrow\widehat{AMB}=\widehat{AMC}=\dfrac{180^O}{2}=90^O\)
=> AM ⊥ BC
10 tháng 3 2023
Đề có sai không bạn , nếu `Delta ABC` là tam giác thường thôi thì không cm đc đâu ạ
CM
1 tháng 5 2019
Kẻ đường cao AH.
Ta có:
Mà BM = CM (vì AM là trung tuyến)
⇒ SAMB = SAMC (đpcm).
N
21 tháng 8 2019
Lam truoc cau a nhe,toi roi
a.Vi tu giac AFME co 3 goc vuong va 2 duong cheo vuong goc voi nhau nen AFDE la hinh vuong.
Goi giao diem giua 2 duong cheo AM va EF do la Q
Suy ra:AQ=FQ nen tam giac AQF la tam giac vuong can hay \(\widehat{AQF}=45^0\left(1\right)\)
Tu giac QFKM co 3 goc vuong va MQ=FQ nen QFKM la hinh vuong.
Suy ra:FK=MK
Ta co:\(FK^2=MK.KC\Rightarrow FK=KC\)
Nen tam giac FKC la tam giac vuong can hay \(\widehat{C}=45^0\left(2\right)\)
Tu (1) va (2) suy ra:AM=MC
Hay AM la duong trung tuyen cua tam giac ABC.
NT
2
16 tháng 4 2022
Xét ΔABC có
AM là đường trung tuyến
AM là đường phân giác
Do đó: ΔABC cân tại A
16 tháng 4 2022
\(\text{Xét }\Delta ABC\text{ có:}\)
\(\left\{{}\begin{matrix}AM\text{ là đường phân giác(gt)}\\AM\text{ là đường trung tuyến(gt)}\end{matrix}\right.\)
\(\Rightarrow\Delta ABC\text{ cân tại A}\)
28 tháng 2 2023
#\(N\)
`a,` Vì Tam giác `ABC` cân tại `A -> AB = AC, `\(\widehat{B}=\widehat{C}\)
`AM` là đường trung tuyến Tam giác `ABC -> BM = MC`
Xét Tam giác `ABM` và Tam giác `ACM` có:
`AB = AC`
\(\widehat{B}=\widehat{C}\)
`BM = MC`
`->` Tam giác `ABM =` Tam giác `ACM (c-g-c)`
`->`\(\widehat{BAM}=\widehat{CAM}\) `(2` góc tương ứng `)`
`-> AM` là phân giác của \(\widehat{BAC}\)
P
Phong
CTVHS
28 tháng 2 2023
Xét tam giác \(\Delta ABM\) và \(\Delta ACM\)
\(AB=AC\left(gt\right)\)
\(\widehat{ABM}=\widehat{ACM}\left(gt\right)\)
\(AM\) chung
\(\Rightarrow\Delta ABM=\Delta ACM\left(c.g.c\right)\)
Từ tam giác bằng nhau trên suy ra:
\(\widehat{BAM}=\widehat{CAM}\) nên \(AM\) là phân giác \(\widehat{BAC}\)
Là phân giác của \(\Delta ABC\)
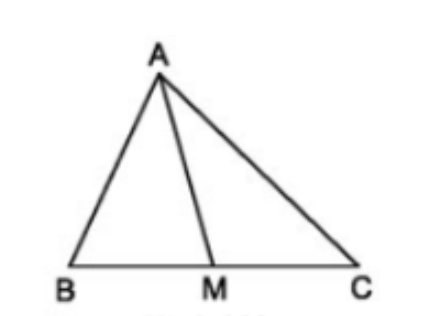
Kẻ đường cao AH
Ta có: SAMB = 0.5.BM.AH
SAMC = 0.5.CM.AH
Mà BM = CM (gt)
Þ SAMB = SAMC (ĐPCM)