Cộng các phân thức sau:
a) và
b) với
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

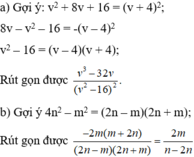

Bài 1 :
a ) Ta có :
\(\left(x+y\right)^2=x^2+y^2+2xy=20+16=36\)
b ) Ta có :
\(x^2+y^2=\left(x+y\right)^2-2xy=64-30=34\)

a) Vì \(u+v=3\sqrt{2}\) và uv=4
nên u,v là hai nghiệm của phương trình: \(x^2-3\sqrt{2}x+4=0\)
\(\Delta=\left(-3\sqrt{2}\right)^2-4\cdot1\cdot4=18-16=2>0\)
Vì \(\Delta>0\) nên phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{3\sqrt{2}-\sqrt{2}}{2}=\sqrt{2}\\x_2=\dfrac{3\sqrt{2}+\sqrt{2}}{2}=2\sqrt{2}\end{matrix}\right.\)
Vậy: \(u=\sqrt{2};v=2\sqrt{2}\)

\(a.A=2015^2=2015\left(2014+1\right)=2015.2014+2015\)
\(B=2014.2016=2014.\left(2015+1\right)=2015.2014+2014\)
Vì \(2015>2014\Rightarrow2015.2014+2015>2015.2014+2014\)
\(\Rightarrow A>B\)
\(b.C=3^{16}-1\)
\(D=8.\left(3^2+1\right).\left(3^4+1\right).\left(3^8+1\right)\)
\(=\left(3^2-1\right)\left(3^2+1\right).\left(3^4+1\right).\left(3^8+1\right)\)
\(=\left(3^4-1\right).\left(3^4+1\right).\left(3^8+1\right)=\left(3^8-1\right)\left(3^8+1\right)=3^{16}-1\)
Vì \(3^{16}-1=3^{16}-1\Rightarrow C=D\)

a, Ta co : A = 1999 * 2001
= ( 2000 - 1 ) *( 2000 + 1 )
= \(2000^2-1\)
Vây A < B
cậu ơi tối mình về mình làm tiếp cho bây giờ mình phải đi hok .


\(3^6\) và \(8^2\)
\(8^2=\left(2^3\right)^2=2^6\)
\(\Rightarrow3^6>8^2\)
a) \(5^3\) và \(3^5\)
Vì : \(5^3=125\)
\(3^5=243\)
Vì 125 < 243 ⇔ \(5^3< 3^5\)
b) \(3^6\) và \(8^2\)
⇒ \(3^6=3^{3.2}=\left(3^3\right)^2=9^2\)
Vì \(9^2>8^2\) ⇔ \(3^6>8^2\)
c) \(16^{19}\) và \(8^{25}\)
⇒ \(16^{19}=\left(2^4\right)^{19}=2^{4.19}=2^{76}\)
⇒ \(8^{25}=\left(2^3\right)^{25}=2^{3.25}=2^{75}\)
Vì \(2^{76}>2^{75}\) ⇔ \(16^{19}>8^{25}\)
d) \(2^{12}\) và \(3^8\)
⇒ \(2^{12}=2^{3.4}=\left(2^3\right)^4=8^4\)
⇒ \(3^8=3^{2.4}=\left(3^2\right)^4=9^4\)
Vì \(8^4< 9^4\) ⇔ \(2^{12}< 3^8\)
e) \(27^{11}\) và \(81^8\)
⇒ \(27^{11}=\left(3^3\right)^{11}=3^{3.11}=3^{33}\)
⇒ \(81^8=\left(3^4\right)^8=3^{4.8}=3^{32}\)
Vì \(3^{33}>3^{32}\) ⇔ \(27^{11}>81^8\)
CHÚC BẠN HỌC TỐT !☕ ⚽ ⚡

Câu a : Ta có :
\(B=\left(2+1\right)\left(2^2+1\right)\left(2^4+1\right)\left(2^8+1\right)\)
\(=\left(2^2-1\right)\left(2^2+1\right)\left(2^4+1\right)\left(2^8+1\right)\)
\(=\left(2^4-1\right)\left(2^4+1\right)\left(2^8+1\right)\)
\(=\left(2^8-1\right)\left(2^8+1\right)\)
\(=2^{16}-1< 2^{16}\)
Vậy \(A>B\)
Câu b : Ta có :
\(A=4\left(3^2+1\right)\left(3^4+1\right)...\left(3^{64}+1\right)\)
\(=\dfrac{8\left(3^2+1\right)\left(3^4+1\right)...\left(3^{64}+1\right)}{2}\)
\(=\dfrac{\left(3^2-1\right)\left(3^2+1\right)\left(3^4+1\right)...\left(3^{64}+1\right)}{2}\)
\(=\dfrac{\left(3^4-1\right)\left(3^4+1\right)...\left(3^{64}+1\right)}{2}\)
\(=\dfrac{...\left(3^{64}-1\right)\left(3^{64}+1\right)}{2}\)
\(=\dfrac{3^{128}-1}{2}< 3^{128}-1\)
Vậy \(A< B\)

a) ta có: \(32^{10}\)=\(\left(2^5\right)^{10}\)= \(2^{50}\)
\(8^{13}\)= \(\left(2^3\right)^{13}\)= \(2^{39}\)
=> \(2^{50}>2^{39}\)=>\(32^{10}>8^{13}\)
b) ta có: \(9^5=\left(3^2\right)^5=3^{10}\)
\(32^2=\left(2^5\right)^2=2^{10}\)
=> \(3^{10}< 2^{10}\)=> \(9^5< 32^2\)
c, ta có \(16^{19}=\left(2^4\right)^{19}=2^{76}\)
\(8^{25}\)\(=\left(2^3\right)^{25}=2^{75}\)
=> \(2^{76}>2^{75}\)=> \(6^{19}>8^{25}\)
d, \(27^{11}=\left(3^3\right)^{11}=3^{33}\)
\(81^8=\left(3^4\right)^8=3^{32}\)
=> \(3^{33}>3^{32}\)=>