Công thức nào sau đây là công thức thấu kính:
A. 1 d + d ' = 1 f
B. 1 f = 1 d + 1 d '
C. 1 d - d ' = 1 f
D. 1 f = 1 d - 1 d '
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(\mathop {\lim }\limits_{d \to {f^ + }} g\left( d \right) = \mathop {\lim }\limits_{d \to {f^ + }} \frac{{df}}{{d - f}} = \mathop {\lim }\limits_{d \to {f^ + }} \left( {df} \right).\mathop {\lim }\limits_{d \to {f^ + }} \frac{1}{{d - f}}\)
Ta có: \(\mathop {\lim }\limits_{d \to {f^ + }} \left( {df} \right) = f\mathop {\lim }\limits_{d \to {f^ + }} d = {f^2};\mathop {\lim }\limits_{d \to {f^ + }} \frac{1}{{d - f}} = + \infty \)
\( \Rightarrow \mathop {\lim }\limits_{d \to {f^ + }} g\left( d \right) = \mathop {\lim }\limits_{d \to {f^ + }} \frac{{df}}{{d - f}} = + \infty \)
Ý nghĩa: Khi vật dần đến tiêu điểm từ phía xa thấu kính đến gần thấu kính thì khoảng cách từ ảnh đến thấu kính dần đến \( + \infty \).
b) \(\mathop {\lim }\limits_{d \to + \infty } g\left( d \right) = \mathop {\lim }\limits_{d \to + \infty } \frac{{df}}{{d - f}} = \mathop {\lim }\limits_{d \to + \infty } \frac{{df}}{{d\left( {1 - \frac{f}{d}} \right)}} = \mathop {\lim }\limits_{d \to + \infty } \frac{f}{{1 - \frac{f}{d}}} = \frac{f}{{1 - 0}} = f\)
Ý nghĩa: Khi khoảng cách từ vật đến thấu kính càng xa thì ảnh tiến dần đến tiêu điểm của ảnh \(\left( {F'} \right)\).

a) Từ hệ thức suy ra d' = φ(d) =
.
b) +) φ(d) =
= +∞ .
Ý nghĩa: Nếu vật thật AB tiến dần về tiêu điểm F sao cho d luôn lớn hơn f thì ảnh của nó dần tới dương vô cực.
+) φ(d) =
= -∞.
Ý nghĩa: Nếu vật thật AB tiến dần về tiêu điểm F sao cho d luôn nhỏ hơn f thì ảnh của nó dần tới âm vô sực.
+) φ(d) =
=
= f.
Ý nghĩa: Nếu vật thật AB ở xa vô cực so với thấu kính thì ảnh của nó ở ngay trên tiêu diện ảnh (mặt phẳng qua tiêu điểm ảnh F' và vuông góc với trục chính).

a) Vẽ hình
O A B B' A' F K
Từ hình vẽ ta thấy: Ảnh là ảnh ảo, lớn hơn vật.
Chứng minh bằng hình học:
Gọi f là tiêu cự, là khoảng cách từ tiêu điểm F đến O.
d là khoảng cách từ vật đến O
d' là khoảng cách từ ảnh đến O
Ta có:
- Tam giác AOB đồng dạng với A'OB' \(\Rightarrow \dfrac{OB}{OB'}=\dfrac{AB}{A'B'}\)(1)
- Tam giác KFO đồng dạng với A'FB' \(\Rightarrow \dfrac{OF}{B'F'}=\dfrac{OK}{A'B'}\)
Mà \(OK=AB\)
\(\Rightarrow \dfrac{OF}{B'F'}=\dfrac{OB}{OB'}\Rightarrow \dfrac{f}{d'+f}=\dfrac{d}{d'}\Rightarrow d'f=dd'+df\Rightarrow d'(f-d)=df\Rightarrow d'=\dfrac{df}{f-d}\) (2)
Từ (1) ta có: \(\dfrac{A'B'}{AB}=\dfrac{d'}{d}\)
Thế d' ở (2) vào ta có: \(\dfrac{A'B'}{AB}=\dfrac{f}{f-d}\)
Vì \(d< f\) nên \(\dfrac{f}{f-d} > 1 \Rightarrow \dfrac{A'B'}{AB}> 1\)
Do đó, ảnh lớn hơn vật.
Các câu khác, bạn vẽ hình và chứng minh tương tự nhé.
Bạn vẽ hình ra, rồi dùng mấy định lý tam giác đồng dạng để chứng minh.

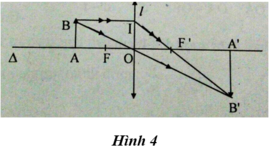
Ta có BI = AO = 2f = 2OF’ => OF’ là đường trung bình của ∆B’BI
=> OB’ = OB => ∆A’B’O = ∆ABO => OA’ = OA = 2f và A’B’ = AB
D = d’ = 2f => d + d’ = 4f => f =(d+d')/4
Đáp án B
Công thức của thấu kính 1 f = 1 d + 1 d '