Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
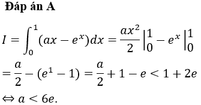
a) \(x\)là số hữu tỉ khi \(a-17\ne0\Leftrightarrow a\ne17\).
b) \(x\)là số hữu tỉ dương khi \(\frac{13}{a-17}>0\Leftrightarrow a-17>0\Leftrightarrow a>17\).
c) \(x\)là số hữu tỉ âm khi \(\frac{13}{a-17}< 0\Leftrightarrow a-17< 0\Leftrightarrow a< 17\).
d) \(x=-1\Rightarrow\frac{13}{a-17}=-1\Rightarrow13=17-a\Leftrightarrow a=4\).
e) \(x>1\Rightarrow\frac{13}{a-17}>1\Leftrightarrow\frac{13-a+17}{a-17}>0\Leftrightarrow\frac{30-a}{a-17}>0\Leftrightarrow17< a< 30\).
f) \(0< x< 1\Rightarrow0< \frac{13}{a-17}< 1\Leftrightarrow a-17>13\Leftrightarrow a>30\).
a) \(x\)là số hữu tỉ khi \(a-17\ne0\Leftrightarrow a\ne17\).
b) \(x\)là số hữu tỉ dương khi \(\frac{13}{a-17}>0\Leftrightarrow a-17>0\Leftrightarrow a>17\).
c) \(x\)là số hữu tỉ âm khi \(\frac{13}{a-17}< 0\Leftrightarrow a-17< 0\Leftrightarrow a< 17\).
d) \(x=-1\Rightarrow\frac{13}{a-17}=-1\Rightarrow13=17-a\Leftrightarrow a=4\).
e) \(x>1\Rightarrow\frac{13}{a-17}>1\Leftrightarrow\frac{13-a+17}{a-17}>0\Leftrightarrow\frac{30-a}{a-17}>0\Leftrightarrow17< a< 30\).
f) \(0< x< 1\Rightarrow0< \frac{13}{a-17}< 1\Leftrightarrow a-17>13\Leftrightarrow a>30\).
1) Để a là 1 số hữu tỉ thì x - 5 khác 0 => x khác 5
2) Để a là 1 số hữu tỉ dương thì x - 5 dương => x - 5 > 0 => x > 5
3) Để a là 1 số hữu tỉ âm thì x - 5 âm => x - 5 < 0 => x < 5
4) Để a = -1 thì x - 5 = -9 => x = -4
5) Để a = 1 thì x - 5 = 9 => x = 14
6) Để a > 1 thì 0 < x - 5 < 9 => 5 < x < 14
7) Để a < -1 thì x - 5 > -9 => x > -4
8) Để 0 < a < 1 thì x - 5 > 9 => x > 14
1) x khác 5
2) x > 5
3) x < 5
4) -4
5) 14
6) a < 14
7) a > -4
8) -4 < a < 14
Đề bài đúng mà bạn..có sai đâu...mình tính vẫn ra được kết quả cuối cùng
