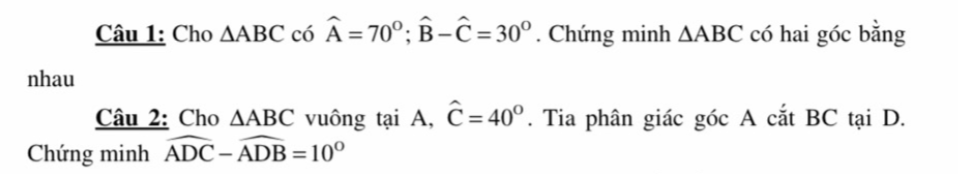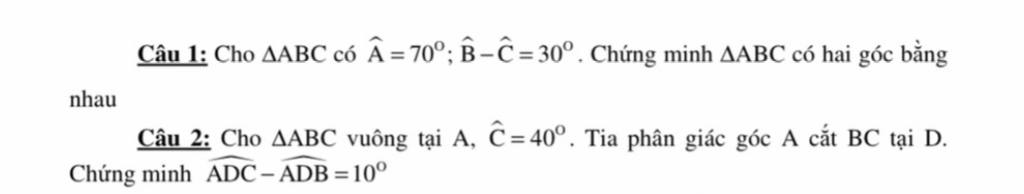Sử dụng tổng 3 góc tam giác
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 1:
\(\widehat{B}+\widehat{C}=110^0\)
\(\Leftrightarrow\widehat{B}=70^0;\widehat{C}=40^0\)
Vậy: ΔABC có hai góc bằng nhau

Câu 1:
\(\left\{{}\begin{matrix}b-c=30\\b+c=110\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=70\\c=40\end{matrix}\right.\)
Vậy: ΔABC có hai góc bằng nhau

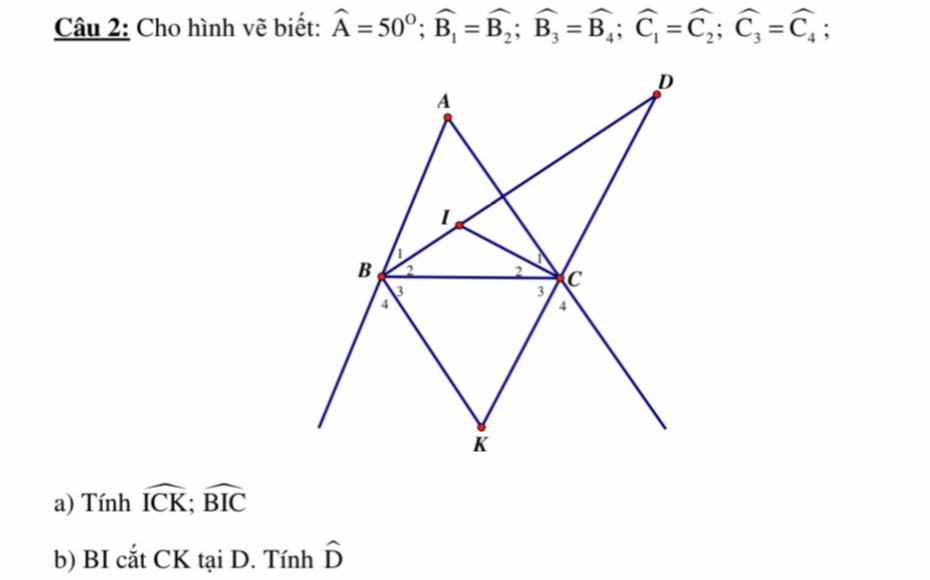
a. Gợi ý: \(\widehat{ICK}=\widehat{C_2}+\widehat{C_3}=\dfrac{1}{2}\left(\widehat{ACB}+\widehat{C}\right)=\dfrac{1}{2}\cdot180^0=90^0\)
\(\widehat{BIC}=180^0-\left(\widehat{B_2}-\widehat{C_2}\right)=180^0-\dfrac{1}{2}\left(\widehat{ABC}+\widehat{ACB}\right)=180^0-\dfrac{1}{2}\left(180^0-\widehat{BAC}\right)=180^0-90^0+\dfrac{1}{2}\widehat{BAC}=90^0+25^0=115^0\)
b. \(\widehat{ICK}=\widehat{D}+\widehat{CID}\Rightarrow\widehat{D}=90^0-\widehat{CID}=90^0-\left(180^0-\widehat{BIC}\right)=...\)


Câu 1:Xét ΔABC có: \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\Rightarrow\widehat{B}+\widehat{C}=110^o\)
Rồi dùng tổng và hiệu tính được góc B và góc C rồi suy ra ĐPCM
Câu 2:
AD là phân giác góc A \(\Rightarrow\widehat{CAD}=\widehat{DAB}=\dfrac{\widehat{BAC}}{2}=45^o\)
Xét ΔACD có: \(\widehat{ADC}+\widehat{ACD}+\widehat{CAD}=180^o\Rightarrow\widehat{ADC}=95^o\)
Ta có: \(\widehat{ADC}+\widehat{ADB}=180^o\Rightarrow\widehat{ADB}=85^o\)
\(\widehat{ADC}-\widehat{ADB}=95^o-85^o=10^o\left(ĐPCM\right)\)

1) Các đỉnh : A, B, C
Các cạnh: AB, BC, AC
Các góc: \(\widehat A,\,\widehat B,\,\widehat C\)
2) AB =3 cm, AC = 3 cm, BC = 3 cm nên các cạnh của tam giác ABC bằng nhau
3) \(\widehat A = 60^0; \widehat B =60^0; \widehat C=60^0\) nên các góc của tam giác ABC bằng nhau và bằng 60o