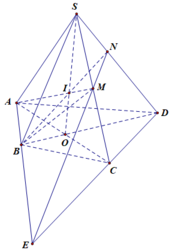
Cho hình chóp S.ABCD có các cạnh AB và CD không song song ; O là giao điểm của hai đường thẳng AC và BD. Giao tuyến của các cặp mặt phẳng (SAC) và (SBD), (SAB) và (SCD) lần lượt là:
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
QT
Quoc Tran Anh Le
Giáo viên
23 tháng 8 2023
Ta có: SD và AB chéo nhau.
Vì AB và SD chéo nhau nên AB không nằm trong mp(SCD).
Vì AB // CD nên AB // mp(SCD).
Vậy (SCD) là mặt phẳng chứa SD và song song với AB.
CM
10 tháng 6 2017
Đáp án A
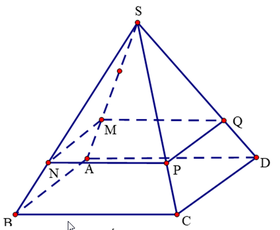
Qua M dựng đường thắng song song AB cắt SB tại N.
Qua M dựng đường thắng song song AD cắt SD tại Q.
Qua N dựng đường thắng song song BC cắt SC tại P.
Ta có M N // A B ⇒ M N // A B C D N P // B C ⇒ N P // A B C D .
⇒ M N P Q / / A B C D .
Tương tự câu 1 ta có tỉ lệ diện tích S M N P Q S A B C D = M N A B 2 = S M S A 2 = 4 9 .
Ta có S A B C D = 10.10 = 100 ⇔ S M N P Q = 100. 4 9 = 400 9
22 tháng 9 2023
Tham khảo:
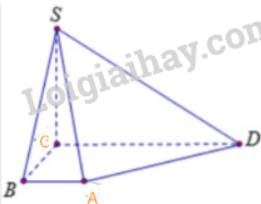
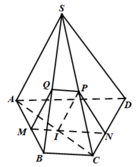
Hình chóp S.ABCD có các mặt bên là hình tam giác nên hình biểu diễn của nó cũng các mặt bên là hình tam giác
Hình thang ABCD có AB//CD và AB=2cm, CD=6cm nên hình biểu diễn của ABCD là một hình thang có đáy CD gấp ba đáy BC
Từ đó, ta vẽ được hình biểu diễn của S.ABCD.
Đáp án B