Giá trị của a để hệ phương trình có nghiệm là:
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\hept{\begin{cases}x+ay=1\\\\-ax+y=a\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=1-ay\\-a\left(1-ay\right)+y=a\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=1-\frac{2a^2}{1+a^2}=\frac{1-a^2}{1+a^2}\\y=\frac{2a}{1+a^2}\end{cases}}\)
Theo đề bài ta có \(\hept{\begin{cases}x< 0\\y< 0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}1-a^2< 0\\2a< 0\end{cases}}\)
\(\Leftrightarrow x< -1\)
a/ Ta xem đây là hệ phương trình 3 ẩn rồi giải bình thường.
\(\hept{\begin{cases}x+ay=1\\-ax+y=a\\2x-y=a+1\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=1-ay\\-a\left(1-ay\right)+y=a\\2\left(1-ay\right)-y=a+1\end{cases}}\)
Tới đây giải tiếp nhé. Không có bút giấy nháp nên giúp tới đây nhé. Chỉ cần thế là được nhé

1:
a)\(\hept{\begin{cases}nx+x=5
\\x+y=1\end{cases}}\Leftrightarrow\hept{\begin{cases}x.\left(n+1\right)=5\left(1\right)\\x+y=1\end{cases}}\)

c) Hệ phương trình đã cho có nghiệm
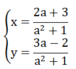
Theo đề bài : x= y
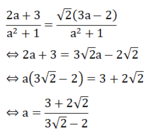
Vậy với 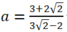 thì hệ phương trình có nghiệm (x; y) thỏa mãn x =
2
y
thì hệ phương trình có nghiệm (x; y) thỏa mãn x =
2
y
x + a y = 1 − a x + y = a ⇔ x = 1 − a y − a 1 − a y + y = a ⇔ x = 1 − a y y a 2 + 1 = 2 a ⇔ x = 1 − a y y = 2 a a 2 + 1 ⇔ x = 1 − a 2 a 2 + 1 y = 2 a a 2 + 1
Để hệ phương trình đã cho có nghiệm thỏa mãn: x < 1; y < 1
⇒ 1 − a 2 a 2 + 1 < 1 2 a a 2 + 1 < 1 ⇔ 1 − a 2 < a 2 + 1 2 a < a 2 + 1 ⇔ 2 a 2 > 0 a − 1 2 > 0 ⇔ a ≠ 0 a ≠ 1
Đáp án:D