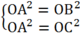Cho ba điểm A(6; 3) ; B(-3; 6) và C(1;-2). Tìm tọa độ tâm đường tròn ngoại tiếp tam giác ABC.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn A.
![]()
Để 3 điểm A, B, C thẳng hàng khi và chi khi A B → , A C → cùng phương
![]()

Chọn B.
Ta có M nằm trên trục Oy nên tọa độ điểm M có dạng M(0; y)
Ba điểm A; B; M thẳng hàng khi ![]() cùng phương với
cùng phương với ![]()
Ta có ![]() . Do đó,
. Do đó, ![]() cùng phương với
cùng phương với
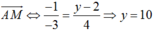
Vậy M(0; 10) .

a) Dựa vào độ dài đã cho của các đoạn thẳng ta nhận thấy rằng MN + NP ≠ MP nên điểm N không nằm giữa hai điểm M và P.
Tương tự, điểm M không nằm giữa hai điểm N và P, điểm P không nằm giữa hai điểm M và N.
Từ đó suy ra ĐPCM.
b) Theo ý a), không có điểm nào nằm giữa hai điểm còn lại nên ba điểm M, N, P không thẳng hàng.
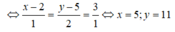
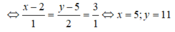

Chọn D.
Gọi O(x0; y0) là tâm đường tròn ngoại tiếp tam giác ABC suy ra:
OA= OB = OC nên