Cho hàm số Để hàm số đạt cực trị tại thỏa mãn thì a thuộc khoảng nào?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Phương pháp:
Dựa vào khái niệm cực trị và các kiến thức liên quan.
Cách giải:
(1) chỉ là điều kiện cần mà không là điều kiện đủ.
VD hàm số y = x3 có y' = 3x2 = 0 ⇔ x = 0. Tuy nhiên x = 0 không là điểm cực trị của hàm số.
(2) sai, khi f''(x0) = 0, ta không có kết luận về điểm x0 có là cực trị của hàm số hay không.
(3) hiển nhiên sai.
Vậy (1), (2), (3): sai; (4): đúng

a. Hàm số y = -2x + 1 có đồ thị là đường thẳng => Không có cực trị ( điều này hiển nhiên )
b) \(y=f\left(x\right)=\frac{x}{3}\left(x-3\right)^2\)
Có:
\(y'=f'\left(x\right)=\frac{1}{3}.\left(x-3\right)^2+\frac{x}{3}.2.\left(x-3\right)=\frac{1}{3}\left(x-3\right)\left(x-3+2x\right)=\left(x-3\right)\left(x-1\right)\)
\(f''\left(x\right)=x-1+x-3=2x-4\)
+) \(f'\left(x\right)=0\Leftrightarrow\orbr{\begin{cases}x=3\\x=1\end{cases}}\)
+) Với x =3 có: \(f''\left(3\right)=2.3-4=2>0\)=> y = f ( x ) đạt cực tiểu tại x = 3.
+ Với x = 1 có: \(f''\left(1\right)=2.1-4=-1< 0\)=> y = f ( x ) đạt cực đại tại x =1
Còn có nhiều cách khác nữa: Vẽ đồ thị, vẽ bảng biến thiên,...

+ Ta có: y' = x2 + 2(m+3)x + 4(m+3)
Yêu cầu của bài toán tường đương y’ =0 có hai nghiệm phân biệt x1; x2 thỏa mãn: -2 < x1< x2
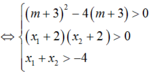
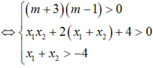
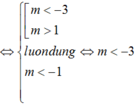
Chọn C

Chọn B
y ' = m x 2 - 2 ( m - 1 ) x + 3 ( m - 2 )
Yêu cầu của bài toán
⇔
y
'
=
0
có hai nghiệm phân biệt
x
1
,
x
2
thỏa mãn:
x
1
+
2
x
2
=
1

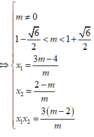

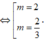

Chọn A
![]()
Hàm số có 2 cực trị ⇔ y ' = 0 có hai nghiệm phân biệt x 1 , x 2 thỏa mãn: - 1 < x 1 < x 2
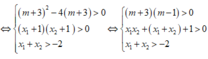
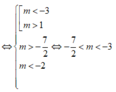

Đáp án A
Ta có y ' = x 2 − 2 a x − 3 a . Để hàm số đặt cực trị tại x 1 , x 2
thì Δ ' = a 2 + 3 a > 0 ⇔ a > 0 a < − 3
Khi đó
x 1 + x 2 = 2 a x 1 x 2 = − 3 a ⇒ x 1 2 + 2 a x 2 + 9 a = x 1 2 + x 1 + x 2 x 2 − 3 x 1 x 2 = x 1 + x 2 2 − 4 x 1 x 2 = 4 a 2 + 12 a
Tương tự ta cũng có x 2 2 + 2 a x 1 + 9 a = 4 a 2 + 12 a . Từ đó suy ra
x 1 2 + 2 a x 2 + 9 a a 2 + a 2 x 2 2 + 2 a x 1 + 9 a = 4 a + 12 a + a 4 a + 12 = 2 ⇔ a 4 a + 12 = 1 ⇔ a = − 4