Cho hàm số có bảng biến thiên trên đoạn như hình vẽ. Có bao nhiêu giá trị nguyên của m để phương trình có đúng 3 nghiệm phân biệt trên khoảng ?

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Ta có: y = x x + 1 = x x + 1 k h i x > 0 − x x + 1 k h i x < 0
Có y ' = 1 x + 1 2 k h i x > 0 − 1 x + 1 2 k h i x < 0
Lập bbt ta được btt như đề bài.
Chú ý: Có thể sử dụng mode 7 đê kiểm tra đáp án.

Chọn D.
Đáp án B sai vì lim x → + ∞ x x + 1 = + ∞ . Đáp án C sai vì y = x x + 1 = x x + 1 2 có y ' ( 0 ) = 1 d d x x x + 1 x = 0 = 1 . Đáp án A sai vì lim x → + ∞ x x + 1 = 0

Chọn C
Xét hàm số g(x) = f 3 ( x ) - 3 f ( x ) trên đoạn [-1;2]
![]()
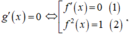
Từ bảng biến thiên, ta có:
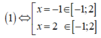
Và ![]() nên f(x) đồng biến trên [-1;2]
nên f(x) đồng biến trên [-1;2]
![]()
![]() nên (2) vô nghiệm
nên (2) vô nghiệm
Do đó, g'(x) = 0 chỉ có nghiệm là x = -1 và x = 2
Ta có ![]()
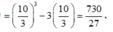
![]()
Vậy ![]()

Đáp án D
Tại -1 hàm số không xác định nên không nghịch biến trên ( - ∞ ; 3 )

Chọn C
Từ bảng biến thiên ta thấy hàm số đã cho nghịch biến trên khoảng C. (-1,1)
Phương pháp:
- Đặt sinx = t, biến đổi điều kiện bài cho về điều kiện của phương trình ẩn t.
- Sử dụng bảng biến thiên để tìm điều kiện của m.
Cách giải:
Phương trình đã cho có đúng 3 nghiệm phân biệt thuộc khoảng − π 2 ; π