Tính tích P = 1 - 1 2 . 1 - 1 3 . 1 - 1 4 . . . . . 1

PT

Pham Trong Bach

7 tháng 4 2017

Tính tích P = 1 - 1 2 . 1 - 1 3 . 1 - 1 4 . . . . . 1 - ...

Đọc tiếp

#Hỏi cộng đồng OLM #Toán lớp 6

1

CM

Cao Minh Tâm

7 tháng 4 2017

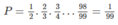
Giải sách bài tập Toán 6 | Giải bài tập Sách bài tập Toán 6

Đúng(0)

NT

nguyễn thu huyền

4 tháng 1 2020 - olm

1^2/1x2x2^2/2x3x4^2/3x5............20^2/19x21 đề bài là tính tích

Bài 2 : Tính tích A = ( 1- 1/1+2)(1-1/1+2+3)(1-1/1+2+3+4).........(1-1/1+2+........+2020)

B = (1/2-1/3)(1/2-1/5)(1/2-1/7).......(1/2-1/99)

#Hỏi cộng đồng OLM #Toán lớp 6

0

TS

Tay súng cừ khôi

28 tháng 6 2016 - olm

tính tích p=(1-1/2)(1-1/3)(1-1/4)...(1-1/99)

#Hỏi cộng đồng OLM #Toán lớp 6

2

NA

Nguyễn Anh Kim Hân

28 tháng 6 2016

\(\left(1-\frac{1}{2}\right)\left(1-\frac{1}{3}\right)\left(1-\frac{1}{4}\right)...\left(1-\frac{1}{99}\right)\)

\(=\frac{1}{2}.\frac{2}{3}.\frac{3}{4}.....\frac{98}{99}\)

\(=\frac{1}{99}\)

Đúng(0)

TS

Tay súng cừ khôi

28 tháng 6 2016

cám ơn bn:)

Đúng(0)

NY

Nijino Yume

30 tháng 3 2019 - olm

Tính tích P=(1-1/2)(1-1/3)(1-1/4)...(1-1/99)

#Hỏi cộng đồng OLM #Toán lớp 6

1

HQ

Huỳnh Quang Sang

30 tháng 3 2019

\(P=\left[1-\frac{1}{2}\right]\left[1-\frac{1}{3}\right]\left[1-\frac{1}{4}\right]...\left[1-\frac{1}{99}\right]\)

\(=\left[\frac{2}{2}-\frac{1}{2}\right]\left[\frac{3}{3}-\frac{1}{3}\right]\left[\frac{4}{4}-\frac{1}{4}\right]...\left[\frac{99}{99}-\frac{1}{99}\right]\)

\(=\frac{1}{2}\cdot\frac{2}{3}\cdot\frac{3}{4}\cdot...\cdot\frac{98}{99}\)

\(=\frac{1\cdot2\cdot3\cdot...\cdot98}{2\cdot3\cdot4\cdot...\cdot99}=\frac{1}{99}\)

Đúng(0)

PH

pham huu tuan

12 tháng 2 2016 - olm

tính các tích với n thuộc N; n>2

a) (1-1/2)*(1-1/3)*(1-1/4)...(1-1/n)

b) (1+1/2)*(1+1/3)*(1+1/4)...(1+1/n)

c) (1-1/2^2)*(1-1/3^2)*(1-1/4^2)...(1-1/n^2)

#Hỏi cộng đồng OLM #Toán lớp 7

0

KD

Khoa Đặng Văn

4 tháng 4 2018 - olm

Tính tích A = ( 1 + 1 /1 × 3 ) × ( 1 + 1 /2 × 4 ) × (1 + 1/3 × 5)...( 1+1/99×101)

#Hỏi cộng đồng OLM #Toán lớp 6

1

KD

Khoa Đặng Văn

4 tháng 4 2018

Giúp mình vs

Đúng(0)

L

lan_nhi

2 tháng 12 2015 - olm

Tính tích Q=(3+1) (3^2+1 ) ( 3^4+1)...(3^2^1997+1)

#Hỏi cộng đồng OLM #Toán lớp 8

0

SD

skt Đạt faker

12 tháng 8 2016 - olm

tính tích P={1-1/2} {1-1/3} {1-1/4}.........{1-1/99}

#Hỏi cộng đồng OLM #Toán lớp 6

2

SB

soyeon_Tiểu bàng giải

12 tháng 8 2016

\(P=\left(1-\frac{1}{2}\right).\left(1-\frac{1}{3}\right).\left(1-\frac{1}{4}\right)...\left(1-\frac{1}{99}\right)\)

\(P=\frac{1}{2}.\frac{2}{3}.\frac{3}{4}...\frac{98}{99}\)

\(P=\frac{1.2.3...98}{2.3.4...99}=\frac{1}{99}\)

Đúng(0)

DL

Dương Lam Hàng

12 tháng 8 2016

Ta có: \(P=\left\{1-\frac{1}{2}\right\}.\left\{1-\frac{1}{3}\right\}....\left\{1-\frac{1}{99}\right\}\)

\(\Rightarrow P=\frac{1}{2}.\frac{2}{3}.........\frac{98}{99}\)\(=\frac{1.2.3...98}{2.3.4...99}=\frac{1}{99}\)

Vậy \(P=\frac{1}{99}\)

Đúng(0)

NT

Nguyễn Thị Anh Phương

9 tháng 3 2016 - olm

tính tích: P=(1-1/2).(1-1/3).(1-1/4).........(1-1/999).(1-1/1000)

#Hỏi cộng đồng OLM #Toán lớp 6

2

NH

Nguyễn Hưng Phát

9 tháng 3 2016

\(P=\left(1-\frac{1}{2}\right).\left(1-\frac{1}{3}\right).................\left(1-\frac{1}{999}\right).\left(1-\frac{1}{1000}\right)\)

\(P=\frac{-1}{2}.\frac{-2}{3}.......................\frac{-998}{999}.\frac{-999}{1000}\)

\(P=\frac{\left(-1\right).\left(-2\right)...............\left(-998\right).\left(-999\right)}{2.3........................999.1000}\)

\(P=\frac{-1}{1000}\)

Đúng(0)

NT

Nguyễn Thị Anh Phương

9 tháng 3 2016

thank you bạn nha

Đúng(0)

TD

Trịnh Diệu Linh

4 tháng 8 2018 - olm

Tính tích

(1-1/2).(1-1/3).(1-1/4)..............(1-1/999).(1-1000)

#Hỏi cộng đồng OLM #Toán lớp 7

5

T

TAKASA

4 tháng 8 2018

\(\left(1-\frac{1}{2}\right).\left(1-\frac{1}{3}\right).\left(1-\frac{1}{4}\right).....\left(1-\frac{1}{999}\right).\left(1-\frac{1}{1000}\right)\)

\(=\frac{1}{2}.\frac{2}{3}.\frac{3}{4}.....\frac{998}{999}.\frac{999}{1000}\)

\(=\frac{1.2.3.....998.999}{2.3.4.....999.1000}\)

\(=\frac{1}{1000}\)

Đúng(0)

KT

Không Tên

4 tháng 8 2018

\(\left(1-\frac{1}{2}\right)\left(1-\frac{1}{3}\right)\left(1-\frac{1}{4}\right)...\left(1-\frac{1}{999}\right)\left(1-\frac{1}{1000}\right)\)

\(=\frac{1}{2}.\frac{2}{3}.\frac{3}{4}....\frac{998}{999}.\frac{999}{1000}\)

\(=\frac{1}{1000}\)

p/s: chúc bạn học tốt

Đúng(0)

LV

Linh Vi

28 tháng 2 2016 - olm

Tính tích sau P=(1-1\2)(1-1\3)(1-1\4)(1-1\5)...(1-1\99)(1-1\100)

#Hỏi cộng đồng OLM #Toán lớp 6

8

HP

Hoàng Phúc

28 tháng 2 2016

P=(1-1/2)(1-1/3)(1-1/4)....(1-1/100)

P=1/2.2/3.3/4.......99/100

P=(1.2.3....99)/(2.3.4...100)=1/100

Vậy P=1/100

Đúng(2)

PH

pham huong ly

14 tháng 8 2016

p=1/100

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP